题目内容
设x,y满足
,则z=x+y的最小值为-7,a=( )
|
| A、1 | B、2 | C、3 | D、4 |
考点:简单线性规划的应用
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定z的最大值.
解答:
 解:约束条件
解:约束条件
的可行域如图:z=x+y的最小值为-7,
直线x=a(y+1)恒过(0,-1),
由
的交点A(-4,-3),
可得直线x=a(y+1)过A(-4,-3)时,x+y取得最小值-7,
此时a=2.
故选:B.
 解:约束条件
解:约束条件
|
直线x=a(y+1)恒过(0,-1),
由
|
可得直线x=a(y+1)过A(-4,-3)时,x+y取得最小值-7,
此时a=2.
故选:B.
点评:本题主要考查线性规划的应用,结合目标函数的几何意义,利用数形结合的数学思想是解决此类问题的基本方法,确定目标函数的斜率关系是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
为了研究性格和血型的关系,抽查80人实验,血型和性格情况如下:O型或A型者是内向型的有18人,外向型的有22人,B型或AB型是内向型的有12人,是外向型的有28人,则有多大的把握认为性格与血型有关系( )
参考数据:
参考数据:
| P(K2≥k0) | 0.5 | 0.10 | 0.010 | 0.001 |
| k0 | 0.455 | 2.706 | 6.635 | 10.828 |
| A、99.9% |
| B、99% |
| C、没有充分的证据显示有关 |
| D、1% |
植树节某班20名同学在一段直线公路一侧植树,每人植一棵,相邻两棵树相距10米.开始时需将树苗集中放置在某一树坑旁边.使每位同学从各自树坑出发前来领取树苗往返所走的路程总和最小,这个最小值为( )米.
| A、1800 | B、2000 |
| C、2200 | D、2400 |
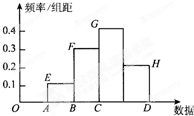 如图,已知样本容量为100,在样本频率分布直方图中,各小长方形的高的比是AE:BF:CG:DH=1:3:4:2,那么第3小组的频率与频数分别为( )
如图,已知样本容量为100,在样本频率分布直方图中,各小长方形的高的比是AE:BF:CG:DH=1:3:4:2,那么第3小组的频率与频数分别为( )| A、0.4,40 |
| B、0.3,30 |
| C、0.2,20 |
| D、0.1,10 |
已知数列:1、-1、1、-1、1、-1…,下列说法正确的是( )
| A、没有通项公式 |
| B、有一个通项公式 |
| C、有多种形式的通项公式 |
| D、以上说法不正确 |
若复数z=
(b∈R,i是虚数单位)是纯虚数,则复数z是( )
| 1+bi |
| 2+i |
A、
| ||
B、-
| ||
| C、-i | ||
| D、i |
直线L1:x+y+1=0,l2:ax-2y+4=0,若L1∥L2,则a等于( )
A、-
| ||
| B、2 | ||
| C、-2 | ||
D、
|
在三角形ABC中,若a=2bcosC,则三角形ABC的形状是( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、等腰或直角三角形 |