题目内容
1.如图,网格纸上小正方形的边长为1,粗线画出的是某个四面体的三视图,则该四面体的表面积为8+8$\sqrt{2}$+4$\sqrt{6}$.
分析 由三视图可知几何体为从边长为4的正方体切出来的三棱锥.作出直观图,计算各棱长求面积.
解答 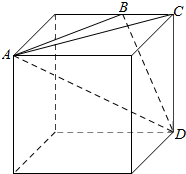 解:由三视图可知几何体为从边长为4的正方体切出来的三棱锥A-BCD.作出直观图如图所示:
解:由三视图可知几何体为从边长为4的正方体切出来的三棱锥A-BCD.作出直观图如图所示:
其中A,C,D为正方体的顶点,B为正方体棱的中点.
∴S△ABC=$\frac{1}{2}×2×4$=4,S△BCD=$\frac{1}{2}×2×4$=4.
∵AC=4$\sqrt{2}$,AC⊥CD,∴S△ACD=$\frac{1}{2}×4×4\sqrt{2}$=8$\sqrt{2}$,
由勾股定理得AB=BD=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,AD=4$\sqrt{3}$.
∴cos∠ABD=$\frac{A{B}^{2}+B{D}^{2}-A{D}^{2}}{2AB•BD}$=-$\frac{1}{5}$,∴sin∠ABD=$\frac{2\sqrt{6}}{5}$.
∴S△ABD=$\frac{1}{2}×2\sqrt{5}×2\sqrt{5}×\frac{2\sqrt{6}}{5}$=4$\sqrt{6}$.
∴几何体的表面积为8+8$\sqrt{2}$+4$\sqrt{6}$.
故答案为8+8$\sqrt{2}$+4$\sqrt{6}$.
点评 本题考查了不规则放置的几何体的三视图和面积计算,作出直观图是解题关键.

练习册系列答案
相关题目
11.设a,b∈R,那么“${π^{\frac{a}{b}}}>π$”是“ea>eb>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.设x1,x2(x1<x2)是函数f(x)=lnx+$\frac{1}{2}$x2-(b-1)x的两个极值点,若b≥$\frac{7}{2}$,则$\frac{{x}_{1}}{{x}_{2}}$的最大值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
13.已知直线y=kx是曲线y=3x的切线,则k的值是( )
| A. | $\frac{1}{3}$ | B. | eln3 | C. | log3e | D. | e |
