题目内容
5. 球O与锐二面角α-l-β的两半平面相切,两切点间的距离为$\sqrt{3}$,O点到交线l的距离为2,则球O的表面积为( )
球O与锐二面角α-l-β的两半平面相切,两切点间的距离为$\sqrt{3}$,O点到交线l的距离为2,则球O的表面积为( )| A. | $\frac{4π}{3}$ | B. | 4π | C. | 12π | D. | 36π |
分析 设球O与平面α,β分别切于点P,Q,过点O作OR⊥l于低能R,连接PR,QR,PQ,设PQ与OR相交于点S,其抽象图如下图所示,则有PO⊥PR,OQ⊥QR,故P,O,Q,R四点共圆,此圆的直径为2,利用三角函数、平面几何知识求解.
解答 解:设球O与平面α,β分别切于点P,Q,
过点O作OR⊥l于低能R,连接PR,QR,PQ,设PQ与OR相交于点S,
其抽象图如下图所示,则有PO⊥PR,OQ⊥QR,故P,O,Q,R四点共圆,此圆的直径为2,
由正弦定理得$\frac{PQ}{sin∠PRQ}=2$,∴$sin∠PRQ=\frac{PQ}{2}=\frac{{\sqrt{3}}}{2}$,
又二面角α-l-β为锐二面角,所以∠PRQ=60°,∠PRO=30°,∴OP=1,即球的半径为1,
球O的表面积为S=4πR2=4π,故选B.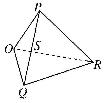
点评 本题考查了球的性质,空间问题转化为平面问题是解题的关键,属于中档题.

练习册系列答案
相关题目
13.抛物线x=4y2的焦点坐标是( )
| A. | (0,1) | B. | (0,-1) | C. | $({-\frac{1}{16},0})$ | D. | $({\frac{1}{16},0})$ |
14.设f(x)=x•lnx,若$f'({x_0})=\frac{3}{2}$,则x0=( )
| A. | $\sqrt{e}$ | B. | $-\sqrt{e}$ | C. | e2 | D. | $\frac{1}{e^2}$ |
15.计算机执行如图的程序,输出的结果是( )


| A. | 3,4 | B. | 7,3 | C. | 3,21 | D. | 21,3 |
 把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵,记M(r,t)表示该数阵中第r行的第t个数,则数阵中的数2 012对应于第45行的第16个数.
把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵,记M(r,t)表示该数阵中第r行的第t个数,则数阵中的数2 012对应于第45行的第16个数.