题目内容
14.已知在正三陵拄A1B1C1-ABC(侧棱垂直于底面,且底面是正三角形)中,D、E分别是棱BC、CC1的中点,AB=AA1=2.(1)证明:BE⊥AB1;
(2)求二面角B-AB1-D的大小.
分析 (1)根据线面垂直的性质定理即可证明BE⊥AB1;
(2)根据二面角的平面角的定义作出二面角的平面角,结合三角形的边角关系即可求二面角B-AB1-D的大小.
解答 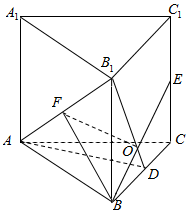 (1)证明:∵在正三陵拄A1B1C1-ABC(侧棱垂直于底面,且底面是正三角形)中,D、E分别是棱BC、CC1的中点,
(1)证明:∵在正三陵拄A1B1C1-ABC(侧棱垂直于底面,且底面是正三角形)中,D、E分别是棱BC、CC1的中点,
∴AD⊥BC,AD⊥面BCC1B1,
则AD⊥BE,
∵AB=AA1=2,
∴△B1BD≌△BCE,
则BE⊥B1D,
∵AD∩B1D=D,
∴BE⊥面ADB1,
∵AB1?面ADB1,
∴BE⊥AB1;
(2)设BE∩B1D=O,
由(1)得BE⊥面ADB1,
取AB1的中点F,连接BF,
∵侧面为正方形,
∴BF⊥AB1,连接OF,
则OF⊥AB1,
即∠OFB是二面角B-AB1-D的平面角,
∵AB=AA1=2.
∴BF=$\sqrt{2}$,BD=1,
DB1=$\sqrt{B{{B}_{1}}^{2}+B{D}^{2}}$=$\sqrt{4+1}$=$\sqrt{5}$,
则OB=$\frac{B{B}_{1}•BD}{{B}_{1}D}=\frac{2×1}{\sqrt{5}}$=$\frac{2}{\sqrt{5}}$,
则sin∠OFB=$\frac{OB}{BF}$=$\frac{\frac{2}{\sqrt{5}}}{\sqrt{2}}$=$\frac{\sqrt{10}}{5}$,
即∠OFB=arcsin$\frac{\sqrt{10}}{5}$
即二面角B-AB1-D的大小为arcsin$\frac{\sqrt{10}}{5}$.
点评 本题主要考查空间直线和直线垂直的证明以及二面角的求解,根据线面垂直的性质定理,以及二面角的平面角的定义作出二面角的平面角是解决本题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
2.若F(c,0)为椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点,椭圆C与直线$\frac{x}{a}+\frac{y}{b}=1$交于A,B两点,线段AB的中点在直线x=c上,则椭圆的离心率为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
19.直线l:2x-y+2=0过椭圆左焦点F1和一个顶点B,则该椭圆的离心率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |