��Ŀ����
9���������н��ۣ���1������f��x��=tanx����������㣻
��2������A={x|y=2x+1}������ B={x|y=x2+x+1}��A��B={��0��1������1��3��}��
��3������$f��x��=\frac{1}{2}sinx+\frac{1}{2}|{sinx}|$��ֵ����[-1��1]��
��4������$f��x��=2sin��2x+\frac{��}{3}��$��ͼ���һ���Գ�����Ϊ$��\frac{��}{3}��0��$��
��5����֪����f��x��=2cosx��������ʵ��x1��x2��ʹ�ö������ʵ��x����f��x1����f��x����f��x2����������|x1-x2|����СֵΪ2�У�
���н�����ȷ������ǣ�1����4����������Ϊ������ȷ����Ŷ����ϣ���
���� ��1��������к���������жϣ�1����
��2�����������ϲ�ȡ�����жϣ�2����
��3��д���ֶκ������ֵ���жϣ�3����
��4��������Ǻ����ĶԳ������жϣ�4����
��5������֪����ʵ��x1��x2��ʹ�ö������ʵ��x����f��x1����f��x����f��x2������ת��Ϊ�����������жϣ�5����
��� �⣺��1����tanx=0����x=k�У�k��Z���ຯ��f��x��=tanx����������㣬�ʣ�1����ȷ��
��2������A={x|y=2x+1}=R������ B={x|y=x2+x+1}=R����A��B=R���ʣ�2������
��3������$f��x��=\frac{1}{2}sinx+\frac{1}{2}|{sinx}|$=$\left\{\begin{array}{l}{sinx��sinx��0}\\{0��sinx��0}\end{array}\right.$����ֵ����[0��1]���ʣ�3������
��4����2x+$\frac{��}{3}=k��$����x=$\frac{k��}{2}-\frac{��}{6}$��k��Z��ȡk=1����x=$\frac{��}{3}$���ຯ��$f��x��=2sin��2x+\frac{��}{3}��$��ͼ���һ���Գ�����Ϊ$��\frac{��}{3}��0��$���ʣ�4����ȷ��
��5���ߺ���f��x��=2cosx������Ϊ2�У�����ʵ��x1��x2��ʹ�ö������ʵ��x����f��x1����f��x����f��x2��������˵��|x1-x2|����СֵΪ$\frac{1}{2}$����=�У��ʣ�5������
����ȷ�������ǣ�1������4����
�ʴ�Ϊ����1����4����
���� ���⿼�����������ж���Ӧ�ã��������Ǻ�����ͼ������ʣ������������������������������е��⣮

 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д�| A�� | $\frac{\sqrt{3}}{2}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{\sqrt{2}}{8}$ |
��������Φ£�m?������ôm�Φ£�
�����m�Φ£�m?�������ɦ�=n����ôm��n��
�����m�ͦ����¡ͦ�����ôm�Φ£�
�����m��n��m�ͦ���n�Φ£���ô���ͦ£�
������ȷ�������ǣ�������
| A�� | �٢� | B�� | �٢� | C�� | �٢� | D�� | �ۢ� |
| A�� | f��-2����f��1����f��3�� | B�� | f��1����f��-2����f��3�� | C�� | f��3����f��-2����f��1�� | D�� | f��-2����f��3����f��1�� |
 ij��ѧ����ѧ��������ڼ����ٲμ�һ����ṫ�������¼�ƻ������У��ѧ�繲��100��ѧ�������Dzμӻ�Ĵ���ͳ����ͼ��ʾ�������ѧ��������ѡ1��ѧ�������μӻ����Ϊ3�ĸ����ǣ�������
ij��ѧ����ѧ��������ڼ����ٲμ�һ����ṫ�������¼�ƻ������У��ѧ�繲��100��ѧ�������Dzμӻ�Ĵ���ͳ����ͼ��ʾ�������ѧ��������ѡ1��ѧ�������μӻ����Ϊ3�ĸ����ǣ�������| A�� | $\frac{1}{10}$ | B�� | $\frac{3}{10}$ | C�� | $\frac{6}{10}$ | D�� | $\frac{7}{10}$ |
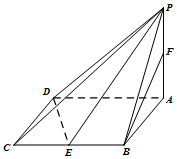 ������P-ABCD�У�����ABCD�DZ߳�Ϊ2�����Σ���BAD=60�㣬PA����ABCD��PA=$\sqrt{3}$��E��F�ֱ�ΪBC��PA���е㣮
������P-ABCD�У�����ABCD�DZ߳�Ϊ2�����Σ���BAD=60�㣬PA����ABCD��PA=$\sqrt{3}$��E��F�ֱ�ΪBC��PA���е㣮