题目内容
已知数列{an}的通项公式是an=(n-
)2+2,若数列﹛an}为递增数列,求实数a的取值范围.
| a |
| 3 |
考点:数列的函数特性
专题:点列、递归数列与数学归纳法
分析:利用二次函数的单调性即可得出.
解答:
解:∵数列﹛an}为递增数列,an=(n-
)2+2,
∴
<1.5,解得a<4.5.
∴实数a的取值范围是(-∞,4.5).
| a |
| 3 |
∴
| a |
| 3 |
∴实数a的取值范围是(-∞,4.5).
点评:本题考查了利用二次函数的单调性解决数列的单调性,属于基础题.

练习册系列答案
相关题目
均值都是5的四组数据条形图如下,将四组数据作比较,错误的是( )
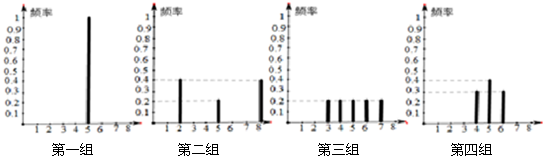

| A、第一组标准差最小 |
| B、第二组极差最大 |
| C、第三组最稳定 |
| D、第三组的方差大于第四组的方差 |