题目内容
如图，在平行四边形ABCD中，2| DE |
| EC |
| AB |
| a |
| AD |
| b |
| a |
| b |
| CP |
-
-
| 3 |
| 4 |
| a |
| 1 |
| 4 |
| b |
-
-
．| 3 |
| 4 |
| a |
| 1 |
| 4 |
| b |
分析：利用向量的共线定理可得到向量
与
关系，再由向量的运算法则可得
=
+
、
=
+
，从而即可得出．
| EP |
| EA |
| CP |
| CE |
| EP |
| EA |
| ED |
| DA |
解答：解：设
=λ
，则
=λ(
+
)=λ(
+
)；
设
=μ
，则
=μ(
-
)=μ(
-
)．
∵
=
-
=
，
∴
=λ(
+
)-μ(
-
)，化为(λ-μ)
+(
λ+μ-
)
=
．
∴
解得λ=μ=
．
∴
=
+
=
+
=-
+
(
+
)=-
+
(-
-
)=-
-
．
故答案为-
-
．
| PE |
| AE |
| PE |
| AD |
| DE |
| b |
| 1 |
| 3 |
| a |
设
| PD |
| BD |
| PD |
| AD |
| AB |
| b |
| a |
∵
| DE |
| PE |
| PD |
| 1 |
| 3 |
| a |
∴
| 1 |
| 3 |
| a |
| b |
| 1 |
| 3 |
| a |
| b |
| a |
| b |
| 1 |
| 3 |
| 1 |
| 3 |
| a |
| 0 |
∴
|
| 1 |
| 4 |
∴
| CP |
| CE |
| EP |
| 2 |
| 3 |
| CD |
| 1 |
| 4 |
| EA |
| 2 |
| 3 |
| AB |
| 1 |
| 4 |
| ED |
| DA |
| 2 |
| 3 |
| a |
| 1 |
| 4 |
| 1 |
| 3 |
| a |
| b |
| 3 |
| 4 |
| a |
| 1 |
| 4 |
| b |
故答案为-
| 3 |
| 4 |
| a |
| 1 |
| 4 |
| b |
点评：熟练掌握向量的共线定理、向量的运算法则是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，在平行四边形ABCD中，下列结论中错误的是（ ）A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
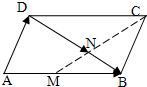如图，在平行四边形ABCD，
如图，在平行四边形ABCD中，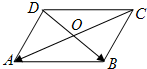
如图，在平行四边形ABCD中，若
如图，在平行四边形OABC中，点O是原点，点A和点C的坐标分别是（3，0）、（1，3），点D是线段AB上的中点．