题目内容
在△ABC中，a=6，B=30°，C=120°，则△ABC的面积是
- A.9
- B.18
- C.
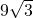
- D.
C
分析：利用三角形的内角和公式求得A=30°，可得△ABC为等腰三角形，直接利用△ABC的面积，求得结果．
解答：∵△ABC中，a=6，B=30°，C=120°，∴A=30°．
故△ABC为等腰三角形，故b=6，则△ABC的面积为
×6×6×sin120°=9
，
故选C．
点评：本题考查三角形中的几何计算，也可以利用正弦定理求解，是一道基础题．
分析：利用三角形的内角和公式求得A=30°，可得△ABC为等腰三角形，直接利用△ABC的面积，求得结果．
解答：∵△ABC中，a=6，B=30°，C=120°，∴A=30°．
故△ABC为等腰三角形，故b=6，则△ABC的面积为
×6×6×sin120°=9，故选C．
点评：本题考查三角形中的几何计算，也可以利用正弦定理求解，是一道基础题．
练习册系列答案
相关题目
在△ABC中，a=6，b=4，C=30°，则△ABC的面积是（ ）
| A、12 | ||
| B、6 | ||
C、12
| ||
D、8
|