题目内容
在 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,求
,求 的值.
的值.
(1) ;(2)
;(2) 或
或 .
.
解析试题分析:本题主要考查解三角形中的正弦定理或余弦定理的运用以及运用三角形公式进行三角变换的能力,考查基本运算能力.第一问,先用正弦定理将边换成角,再利用 将
将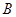 角换成
角换成 ,展开后解方程求角;第二问,利用第一问的结论,利用余弦定理得到
,展开后解方程求角;第二问,利用第一问的结论,利用余弦定理得到 和
和 的关系式,分情况讨论利用正弦定理求
的关系式,分情况讨论利用正弦定理求 .
.
试题解析:(Ⅰ) 由题意及正弦定理得 ,
,
即 .因为
.因为 ,所以
,所以 ,从而得
,从而得 . 6分
. 6分
(Ⅱ)由 及余弦定理得
及余弦定理得 ,即
,即 ,所以
,所以 .
.
当 时,
时,
又 ,
,
故 ,
,
所以 .
.
当 时,同理得
时,同理得 .
.
综上所述, 或
或 . 14分
. 14分
考点:1.正弦定理;2.余弦定理;3.两角和与差的正弦公式.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 中,已知
中,已知 ,
, 是
是 边上的一点,
边上的一点,

 的值;
的值; 的值。
的值。 中
中 ,
, 为线段
为线段 上一点,且
上一点,且 ,线段
,线段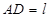 .
.
 ,
,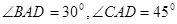 ,试求线段
,试求线段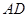 的长.
的长. 的内角
的内角 所对的边长分别为
所对的边长分别为 ,且满足
,且满足
 的大小;
的大小; ,
, 边上的中线
边上的中线 的长为
的长为 ,求
,求 的顶点
的顶点 ,顶点
,顶点 在直线
在直线 上;
上; 求点
求点 ,且
,且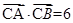 ,求角
,求角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,满足
,满足 .
. ,且
,且 ,求△ABC的面积.
,求△ABC的面积. 中,角
中,角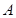 、
、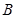 、
、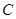 的对边分别为
的对边分别为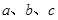 ,且
,且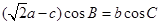 .
.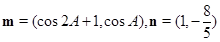 ,且
,且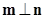 ,求
,求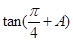 的值.
的值. 中,BC=a,AC=b,a,b是方程
中,BC=a,AC=b,a,b是方程
 的两个根,且2COS(A+B)=1.
的两个根,且2COS(A+B)=1.