题目内容
如图,在 中,已知
中,已知 ,
, 是
是 边上的一点,
边上的一点,

(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值。
的值。
(1)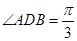 ;(2)
;(2)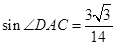 .
.
解析试题分析:本题主要考查解三角形中的正弦定理、余弦定理的应用,考查基本的运算能力,考查分析问题解决问题的能力.法一:第一问,在 中利用余弦定理求边
中利用余弦定理求边 的长,利用
的长,利用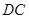 的长度,可以求出
的长度,可以求出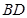 的长,通过
的长,通过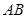 ,
,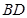 ,角
,角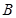 可以判断出
可以判断出 为等边三角形,所以
为等边三角形,所以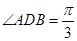 ,
,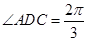 ,
,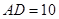 ;第二问,在
;第二问,在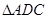 中,利用余弦定理,可以求出
中,利用余弦定理,可以求出 的余弦,再利用平方关系求出
的余弦,再利用平方关系求出 ;法二:第一问,在
;法二:第一问,在 中利用正弦定理求出
中利用正弦定理求出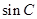 ,从而利用平方关系求出
,从而利用平方关系求出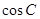 ,在
,在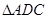 中,利用余弦定理求出
中,利用余弦定理求出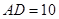 ,再确定
,再确定 为等比三角形,从而得到
为等比三角形,从而得到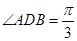 ,
,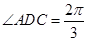 ;第二问,在
;第二问,在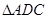 中,再利用正弦定理求出
中,再利用正弦定理求出 的值.
的值.
试题解析:法一:(Ⅰ)由余弦定理
得 ,
,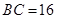 或
或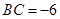 (舍去),
(舍去),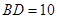 ,
, 为等边三角形,
为等边三角形,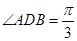 ,
,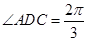 , 8分
, 8分
(Ⅱ) 得
得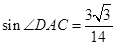 12分
12分
法二:(Ⅰ)由正弦定理可得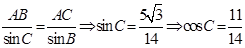
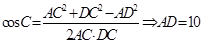 ,
,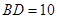 ,
, 为等比三角形,
为等比三角形,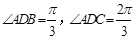 8分
8分
(Ⅱ)由正弦定理可得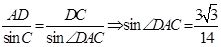 12分
12分
考点:1.余弦定理;2.正弦定理;3.平方关系.

练习册系列答案
相关题目
 sin xcos x+2cos2x+m在区间
sin xcos x+2cos2x+m在区间 上的最大值为2.
上的最大值为2. ,求边长a.
,求边长a. .
.
 表示
表示 的面积;
的面积; 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, .若
.若 ,
, .
. 的最小值.
的最小值. ABC中,角A,B,C的对边分别为a,b,c, 若向量
ABC中,角A,B,C的对边分别为a,b,c, 若向量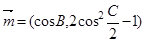 与向量
与向量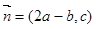 共线.
共线.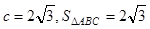 ,求a,b的值.
,求a,b的值. 分别为角
分别为角 所对的三边,已知
所对的三边,已知
 的值
的值 ,求边
,求边 的长.
的长.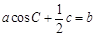 .
.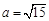 ,
,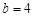 ,求边c的大小.
,求边c的大小.
 C
C 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 .
. 的大小;
的大小; ,求
,求 的值.
的值.