题目内容
在△ABC中,角A、B、C所对的边分别为a、b、c,且b2+c2=a2+bc.
(1)求角A的大小;(2)若sinB·sinC=sin2A,试判断△ABC的形状.
(1)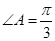 ;(2)
;(2)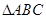 是等边三角形.
是等边三角形.
解析试题分析:(1)经审题,由条件 得到提示,在三角形
得到提示,在三角形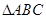 中,若求角
中,若求角 的大小,则用余弦定理
的大小,则用余弦定理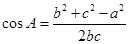 可求得;(2)解法一:根据正弦定理,将条件
可求得;(2)解法一:根据正弦定理,将条件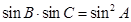 转化为
转化为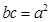 ,将其代入已知条件
,将其代入已知条件 可解得
可解得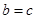 ,从而有
,从而有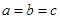 ,故
,故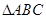 为等边三角形;解法二:由(1)结论得
为等边三角形;解法二:由(1)结论得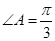 ,那么在
,那么在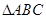 中有
中有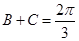 ,则
,则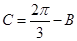 ,由条件
,由条件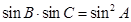 可得
可得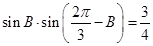 ,由三角恒等变换公式可得
,由三角恒等变换公式可得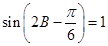 ,所以
,所以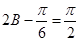 ,解得
,解得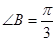 ,从而有
,从而有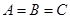 ,故
,故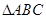 为等边三角形.
为等边三角形.
试题解析:(1)由已知得 ,
,
又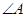 是
是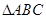 的内角,
的内角, . 5分
. 5分
(2)由正弦定理,得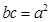
又 ,
,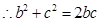
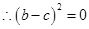 ,即
,即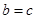 .
.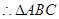 是等边三角形. 12分
是等边三角形. 12分
考点:正弦定理、余弦定理.

练习册系列答案
相关题目
 .
.
 表示
表示 的面积;
的面积;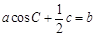 .
.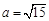 ,
,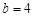 ,求边c的大小.
,求边c的大小.
 C
C 两个小岛相距10
两个小岛相距10 ,船O将保持观望A岛和B岛所成的视角为
,船O将保持观望A岛和B岛所成的视角为 ,现从船O上派下一只小艇沿
,现从船O上派下一只小艇沿 方向驶至
方向驶至 处进行作业,且
处进行作业,且 .设
.设

 分别表示
分别表示 和
和 ,并求出
,并求出 的距离为
的距离为 ,求BD的最大值.
,求BD的最大值. 中,已知
中,已知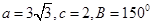 ,求边
,求边 的长及
的长及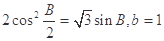 .
.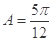 ,求边c的大小;
,求边c的大小; 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 .
. 的大小;
的大小; ,求
,求 的值.
的值. 中,
中,
 的值;
的值; 的值.
的值.