题目内容
已知A(7,8),B(10,4),C(2,4),则△ABC的面积是 .
考点:两点间距离公式的应用,点到直线的距离公式
专题:直线与圆
分析:根据三角形的面积公式求出底和高即可.
解答:
 解:∵B(10,4),C(2,4),
解:∵B(10,4),C(2,4),
∴B,C所在的直线方程为y=4,且BC=10-2=8,
则点A到直线y=4的距离d=8-4=4,
故三角形的高为4,
则△ABC的面积是S=
×8×4=16,
故答案为:16
 解:∵B(10,4),C(2,4),
解:∵B(10,4),C(2,4),∴B,C所在的直线方程为y=4,且BC=10-2=8,
则点A到直线y=4的距离d=8-4=4,
故三角形的高为4,
则△ABC的面积是S=
| 1 |
| 2 |
故答案为:16
点评:本题主要考查三角形面积的计算,根据条件求出三角形的底和高的长度是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
底面是正方形,侧面是全等的等腰三角形的四棱锥,其5个顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A、
| ||
| B、16π | ||
| C、9π | ||
D、
|
对于平面α,β,γ和直线a,b,m,n,下列命题中真命题是( )
| A、若α∥β,α∩γ=a,β∩γ=b,则a∥b |
| B、若a∥b,b⊆α,则a∥α |
| C、若a⊆β,b⊆β,a∥α,b∥α,则β∥α |
| D、若a⊥m,a⊥n,m⊆α,n⊆α,则a⊥α |
 如图Rt△O′A′B′是一平面图形的直观图,斜边O′B′=2,则这个平面图形的面积是
如图Rt△O′A′B′是一平面图形的直观图,斜边O′B′=2,则这个平面图形的面积是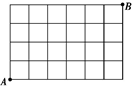 某市新城区有7条南北向街道,5条东西向街道(如图).
某市新城区有7条南北向街道,5条东西向街道(如图).