题目内容

9．如图，飞机的航线和山顶在同一个铅垂面内，若飞机的高度为海拔18km，速度为1 000km/h，飞行员先看到山顶的俯角为30°，经过1min后又看到山顶的俯角为75°，则山顶的海拔高度为（精确到0.1km，参考数据：$\sqrt{3}$≈1.732）（　　）
A．11.4 kmB．6.6 kmC．6.5 kmD．5.6 km

分析 根据题意求得∠ACB和AB的长，然后利用正弦定理求得BC，最后利用BC•sin75°求得问题的答案．

解答 解：在△ABC中，∠BAC=30°，∠ACB=75°-30°=45°，AB=1000×$\frac{1}{60}$=$\frac{50}{3}$．
根据正弦定理，$\frac{\frac{50}{3}}{sin45°}=\frac{BC}{sin30°}$，
∴BC=$\frac{25}{3}$$\sqrt{2}$．
BC•sin75°=$\frac{25}{3}\sqrt{2}$×sin（45°+30°）≈11.5．
所以，山顶P的海拔高度为h=18-11.4=6.5（千米）．
故选：C．

点评 本题主要考查了解三角形问题的应用．注意把实际问题与三角函数的知识相联系，建立相应的数学模型．

练习册系列答案
相关题目
9．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与y轴交于B1，B2两点，F1为椭圆C的左焦点，且△F1B1B2是边长为2的等边三角形．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设直线x=my+1与椭圆C交于P，Q两点，点P关于x轴的对称点为P1（P1与Q不重合），则直线P1Q与x轴交于点H，求△PQH面积的取值范围．
20．设tanα，tanβ是方程x2+3x-2=0的两个根，则tan（α+β）的值为（　　）
A．-3B．-1C．1D．3
17．已知向量$\overrightarrow m=（sinx，-1）$，向量$\overrightarrow n=（\sqrt{3}cosx，-\frac{1}{2}）$，函数$f（x）=（\overrightarrow m+\overrightarrow n）•\overrightarrow m$．
（1）求f（x）的解析式及单调增区间；
（2）已知a，b，c分别为△ABC内角A，B，C的对边，A为锐角，a=2$\sqrt{3}$，c=4，且f（A）恰是f（x）在$[{0，\frac{π}{2}}]$上的最大值，求A，b和△ABC的面积S．
4．已知函数f（x）=$\sqrt{2}sinωxcosωx+\sqrt{2}{cos^2}ωx-\frac{{\sqrt{2}}}{2}（{ω＞0}）$，若x=$\frac{π}{4}$是函数f（x）的一条对称轴，则实数ω的值可以是（　　）
A．1B．$\frac{1}{2}$C．$\frac{1}{4}$D．$\frac{1}{8}$
14．设数列{an}，{bn}，{cn}，已知${a_1}=4，{b_1}=3，{c_1}=5，{a_{n+1}}={a_n}，{b_{n+1}}=\frac{{{a_n}+{c_n}}}{2}$，${c_{n+1}}=\frac{{{a_n}+{b_n}}}{2}（{n∈{N^*}}）$．
（1）求b2，c2，b3，c3；
（2）求数列{cn-bn}的通项公式；
（3）求证：对任意n∈N*，bn+cn为定值．
1．已知集合A={x|0＜x＜2}，B={x|1-x2＞0}，则A∩（∁RB）=（　　）
A．{x|0≤x≤1}B．{x|1≤x＜2}C．{x|-1＜x≤0}D．{x|0≤x＜1}
18．如果$sinα=\frac{2}{3}，cosβ=-\frac{1}{4}，α$与β为同一象限角，则sin（α-β）=$\frac{5\sqrt{3}-2}{12}$．
19．如图中的网格纸是边长为1的小正方形，在其上用粗线画出了一四棱锥的三视图，则该四棱锥的体积为（　　）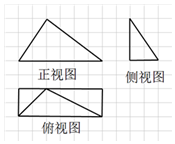
A．12B．8C．6D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网