题目内容
2．某几何体的三视图如图所示，则它的体积是（ ）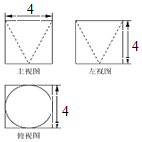
| A． | $8-\frac{2π}{3}$ | B． | $64-\frac{16π}{3}$ | C． | $8-\frac{π}{3}$ | D． | $64-\frac{12π}{3}$ |
分析 由题意，几何体的直观图是正方体挖去一个圆锥，即可求出体积．
解答 解：由题意，几何体的直观图是正方体挖去一个圆锥，
体积为${4}^{3}-\frac{1}{3}π•{2}^{2}•4$=64-$\frac{16π}{3}$，
故选B．
点评 本题考查的知识点是由三视图求体积，其中由已知中的三视图判断出几何体的形状，及棱长，高等几何量是解答的关键．
练习册系列答案
名校课堂系列答案
相关题目
10．如图，输入n=5时，则输出的S=（ ）
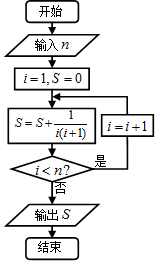
| A． | $\frac{3}{4}$ | B． | $\frac{4}{5}$ | C． | $\frac{5}{6}$ | D． | $\frac{6}{7}$ |
7．已知f（x）=${log}_{2}|x|{+3}^{|x|}$，则f（x2-1）＜3的解集为（ ）
| A． | （-$\sqrt{2}$，-1）∪（-1，0）∪（0，1）∪（1，$\sqrt{2}$） | B． | （-$\sqrt{2}$，0）∪（0，$\sqrt{2}$） | ||
| C． | （-$\sqrt{2}$，$\sqrt{2}$） | D． | （-$\sqrt{2}$，-1）∪（1，$\sqrt{2}$） |