题目内容
16．若函数y=-ax与y=$\frac{b}{x}$在（-∞，0）上都是减函数，则y=ax2+bx在（-∞，0）上是（ ）| A． | 减函数 | B． | 增函数 | C． | 先增后减 | D． | 先减后增 |
分析 利用函数的单调性判断a，b的范围，然后利用二次函数的性质判断选项即可．
解答 解：函数y=-ax与y=$\frac{b}{x}$在（-∞，0）上都是减函数，
可得a＞0，b＞0，则y=ax2+bx的开口向上，对称轴：x=-$\frac{b}{2a}$＜0，
则y=ax2+bx在（-∞，0）上是先减后增．
故选：D．
点评 本题考查函数的单调性的判断与应用，二次函数的简单性质的应用，是基础题．
练习册系列答案
相关题目
4．若方程（$\frac{1}{4}$）x+（$\frac{1}{2}$）x-1+a=0有正数解，则实数a的取值范围是（ ）
| A． | （0，1） | B． | （-3，0） | C． | （-2，0） | D． | （-1，0） |
1．已知集合M={0，1，2，3}，N={x|y=$\sqrt{2-x}$}，则M∩N=（ ）
| A． | {0，1} | B． | {1，2} | C． | {0，1，2} | D． | {2，3，4} |
8．已知函数f（x）是定义在R上的偶函数，且对任意x∈R，都有f（x-1）=f（x+3）．当x∈[4，5]时，f（x）=2x+1，设函数f（x）在区间[-2，0]上的反函数为f-1（x），则f-1（19）的值为（ ）
| A． | -log23 | B． | -2log23 | C． | 1-log23 | D． | 3-2log23 |
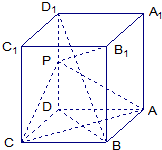如图，长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，点P为DD1的中点．求：