题目内容
17.求曲线y=cosx在点A($\frac{π}{6}$,$\frac{\sqrt{3}}{2}$)处的切线方程.分析 求出原函数的导函数,得到函数在x=$\frac{π}{6}$时的导数,然后由直线方程的点斜式得答案.
解答 解:由y=cosx,得y′=-sinx,
∴$y′{|}_{x=\frac{π}{6}}=-sin\frac{π}{6}=-\frac{1}{2}$,
∴曲线y=cosx在点A($\frac{π}{6}$,$\frac{\sqrt{3}}{2}$)处的切线方程为y-$\frac{\sqrt{3}}{2}=-\frac{1}{2}(x-\frac{π}{6})$,
即$6x+12y-6\sqrt{3}-π=0$.
点评 本题考查利用导数研究过曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.

练习册系列答案
相关题目
 ,且
,且 ,则当
,则当 时,
时, 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
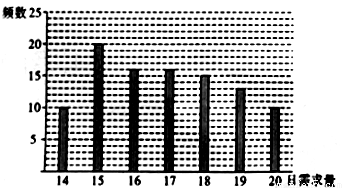
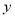 (单位:元)关于当天需求量
(单位:元)关于当天需求量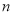 (单位:个,
(单位:个,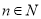 )的函数解析式;
)的函数解析式;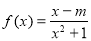 是奇函数,
是奇函数, 是偶函数.
是偶函数.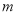 ,
,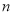 的值;
的值;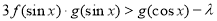 对任意
对任意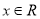 恒成立,求实数
恒成立,求实数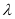 的取值范围.
的取值范围.