题目内容
如图,在平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.(1)求二面角E-AB-D的大小;
(2)求四面体ABDE的表面积.
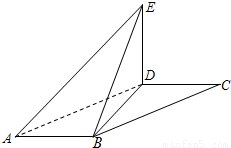
【答案】分析:(1)要求二面角E-AB-D的大小,先利用题设条件,推导出∠DBE即为二面角E-AB-D的平面角.再由题设条件求出二面角的余弦值,由此能求出二面角的大小.
(2)由题设条件分别求出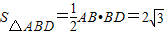 .S△BDC=
.S△BDC=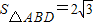 ,
,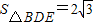 ,
,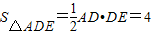 .由此能求出四面体ABDE的表面积.
.由此能求出四面体ABDE的表面积.
解答:解:(1)在△EBD中,
∵∠DAB=60°,AB=2,AD=4,
∴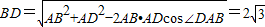 .
.
∴AB2+BD2=AD2,∴AB⊥BD.
∵平面EBD⊥平面ABD,∴AB⊥平面BDE,∴AB⊥BE.
∴∠DBE即为二面角E-AB-D的平面角.
又∵CD⊥BD,∴ED⊥BD,而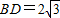 ,
,
DE=DC=AB=2,
∴在Rt△BDE中,cos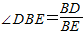 =
=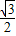 ,
,
∴∠DBE=30°.
(2)由(1)知:AB⊥BD,
∴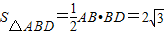 .
.
又∵S△BDC=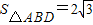 ,而△EBD即为△BDC,
,而△EBD即为△BDC,
∴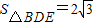 .
.
又∵AB⊥BE,BE=BC=AD=4,∴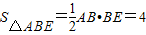 .
.
又DE⊥AD,∴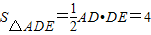 .
.
故四面体ABDE的表面积为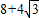 .
.
点评:本题考查二面角的求法,考查四面体的表面积的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.
(2)由题设条件分别求出
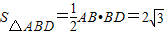 .S△BDC=
.S△BDC=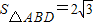 ,
,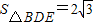 ,
,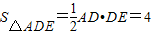 .由此能求出四面体ABDE的表面积.
.由此能求出四面体ABDE的表面积.解答:解:(1)在△EBD中,
∵∠DAB=60°,AB=2,AD=4,
∴
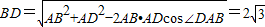 .
.∴AB2+BD2=AD2,∴AB⊥BD.
∵平面EBD⊥平面ABD,∴AB⊥平面BDE,∴AB⊥BE.
∴∠DBE即为二面角E-AB-D的平面角.
又∵CD⊥BD,∴ED⊥BD,而
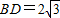 ,
,DE=DC=AB=2,
∴在Rt△BDE中,cos
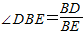 =
=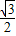 ,
,∴∠DBE=30°.
(2)由(1)知:AB⊥BD,
∴
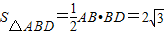 .
.又∵S△BDC=
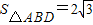 ,而△EBD即为△BDC,
,而△EBD即为△BDC,∴
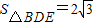 .
.又∵AB⊥BE,BE=BC=AD=4,∴
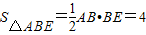 .
.又DE⊥AD,∴
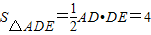 .
.故四面体ABDE的表面积为
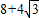 .
.点评:本题考查二面角的求法,考查四面体的表面积的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,下列结论中错误的是( )
如图,在平行四边形ABCD中,下列结论中错误的是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
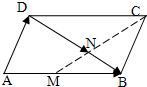 如图,在平行四边形ABCD,
如图,在平行四边形ABCD, 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,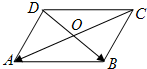 如图,在平行四边形ABCD中,若
如图,在平行四边形ABCD中,若 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.