题目内容
13.数列{an}是等比数列,前n项和为Sn,若a1+a2=2,a2+a3=-1,则$\lim_{n→∞}{S_n}$=$\frac{8}{3}$.分析 利用等比数列的通项公式可得a1,q,再利用$\lim_{n→∞}{S_n}$=$\frac{{a}_{1}}{1-q}$即可得出.
解答 解:设等比数列{an}的公比为q,∵a1+a2=2,a2+a3=-1,
∴q=-$\frac{1}{2}$,a1(1-$\frac{1}{2}$)=2,解得a1=4.
则$\lim_{n→∞}{S_n}$=$\frac{{a}_{1}}{1-q}$=$\frac{8}{3}$.
故答案为:$\frac{8}{3}$.
点评 本题考查了等比数列的通项公式与求和公式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
3.某供货商计划将某种大型节日商品分别配送到甲、乙两地销售.据以往数据统计,甲、乙两地该商品需求量的频率分布如下:
甲地需求量频率分布表示:
乙地需求量频率分布表:
以两地需求量的频率估计需求量的概率
(Ⅰ)若此供货商计划将10件该商品全部配送至甲、乙两地,为保证两地不缺货(配送量≥需求量)的概率均大于0.7,问该商品的配送方案有哪几种?
(Ⅱ)已知甲、乙两地该商品的销售相互独立,该商品售出,供货商获利2万元/件;未售出的,供货商亏损1万元/件.在(Ⅰ)的前提下,若仅考虑此供货商所获净利润,试确定最佳配送方案.
甲地需求量频率分布表示:
| 需求量 | 4 | 5 | 6 |
| 频率 | 0.5 | 0.3 | 0.2 |
| 需求量 | 3 | 4 | 5 |
| 频率 | 0.6 | 0.3 | 0.1 |
(Ⅰ)若此供货商计划将10件该商品全部配送至甲、乙两地,为保证两地不缺货(配送量≥需求量)的概率均大于0.7,问该商品的配送方案有哪几种?
(Ⅱ)已知甲、乙两地该商品的销售相互独立,该商品售出,供货商获利2万元/件;未售出的,供货商亏损1万元/件.在(Ⅰ)的前提下,若仅考虑此供货商所获净利润,试确定最佳配送方案.
4.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1和F2,以F1F2为直径的圆与双曲线的一个交点为P,若|PF1|=a,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\sqrt{10}$ | D. | $\sqrt{2}$ |
14.已知O是△ABC的外心,∠C=45°,若$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$(m,n∈R),则m+n的取值范围是( )
| A. | [$-\sqrt{2}$,$\sqrt{2}$] | B. | [$-\sqrt{2}$,1) | C. | [$-\sqrt{2}$,-1) | D. | (1,$\sqrt{2}$] |
15.设α,β∈[0,π],且满足sinαcosβ-cosαsinβ=1,则cos(2α-β)的取值范围为( )
| A. | [0,1] | B. | [-1,0] | C. | [-1,1] | D. | $[{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}}]$ |
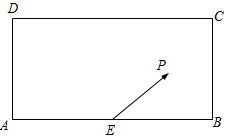 某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛,在E处按$\overrightarrow{EP}$方向释放机器人甲,同时在A处按某方向释放机器人乙,设机器人乙在Q处成功拦截机器人甲.若点Q在矩形区域ABCD内(包含边界),则挑战成功,否则挑战失败.
某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛,在E处按$\overrightarrow{EP}$方向释放机器人甲,同时在A处按某方向释放机器人乙,设机器人乙在Q处成功拦截机器人甲.若点Q在矩形区域ABCD内(包含边界),则挑战成功,否则挑战失败.