Question

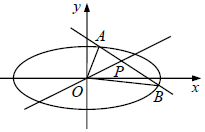
8．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左右焦点分别为F₁，F₂，离心率为$\frac{1}{2}$，点A在椭圆C上，|AF₁|=2，∠F₁AF₂=60°，过F₂与坐标轴不垂直的直线l与椭圆C交于P，Q两点，N为P，Q的中点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）已知点$M（0，\frac{1}{8}）$，且MN⊥PQ，求直线MN所在的直线方程．

Answer 1

分析 （Ⅰ）通过离心率以及由余弦定理，转化求解椭圆C的方程．
（Ⅱ）因为直线PQ的斜率存在，设直线方程为y=k（x-1），P（x₁，y₁），Q（x₂，y₂），联立$\left\{\begin{array}{l}y=k（x-1）\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$，由韦达定理求解N，M的坐标，MN⊥PQ，转化求解即可．

解答 解：（Ⅰ）由$e=\frac{1}{2}$，得a=2c，
因为|AF₁|=2，|AF₂|=2a-2，
由余弦定理得$|A{F_1}{|^2}+|A{F_2}|-2|A{F_1}|•|A{F_2}|cosA=|{F_1}{F_2}{|^2}$，
解得c=1，a=2，
∴b²=a²-c²=3，
∴椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$．
（Ⅱ）因为直线PQ的斜率存在，设直线方程为y=k（x-1），P（x₁，y₁），Q（x₂，y₂），
联立$\left\{\begin{array}{l}y=k（x-1）\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$整理得（3+4k²）x²-8k²x+4k²-12=0，
由韦达定理知${x_1}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}}$，${y_1}+{y_2}=k（{x_1}+{x_2}）-2k=\frac{-6k}{{3+4{k^2}}}$，
此时$N（\frac{{4{k^2}}}{{3+4{k^2}}}，\frac{-3k}{{3+4{k^2}}}）$，又$M（0，\frac{1}{8}）$，则${k_{MN}}=\frac{{\frac{1}{8}+\frac{3k}{{3+4{k^2}}}}}{{0-\frac{{4{k^2}}}{{3+4{k^2}}}}}=-\frac{{24k+3+4{k^2}}}{{32{k^2}}}$，
∵MN⊥PQ，∴${k_{MN}}=-\frac{1}{k}$，得到$k=\frac{1}{2}$或$\frac{3}{2}$．
则k_MN=-2或${k_{MN}}=-\frac{2}{3}$，MN的直线方程为16x+8y-1=0或16x+24y-3=0．

点评 本题考查直线与椭圆的位置关系的应用，椭圆方程的求法，考查计算能力．