题目内容
9.已知函数y=f(x)(x∈R)满足f(x)=2f(x-2),且x∈[-1,1]时,f(x)=|x|-1,则当x∈[-9,0)∪(0,9]时,y=f(x)与$g(x)={log_{\frac{1}{3}}}|x|$的图象的交点的个数为16.分析 由函数y=f(x)(x∈R)满足f(x)=2f(x-2),得y=f(x)(x∈R)满足f(x+2)=2f(x),
利用此条件作出函数y=f(x)与g(x)的图象,利用图象得到函数的交点个数即可.
解答 解:∵函数y=f(x)(x∈R)满足f(x)=2f(x-2),
∴y=f(x)(x∈R)满足f(x+2)=2f(x),且x∈[-1,1]时,f(x)=|x|-1,
∵f(x)与g(x)都为偶函数,只看x>0时的图象交点个数即可,
∴f(x)在区间[1,3]的图象是由函数f(x)在区间[-1,1]图象作振幅扩大2倍的变换,而f(x)在区间[3,5]的图象是由函数f(x)在区间[1,3]图象作振幅扩大2倍的变换,依此类推;
分别作出函数y=f(x)(x>0)与g(x)=log4x(x>0)的图象如图: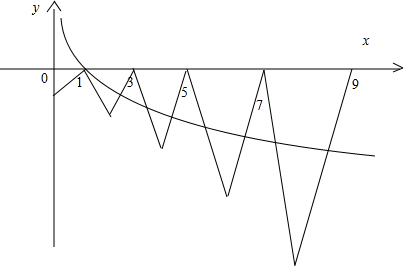
由图象可知当x>0时,y=f(x)与g(x)=log4x的图象的交点个数为8个,
由偶函数的性质知共有16个交点.
故答案为:16.
点评 本题主要考查函数图象的交点个数问题,利用条件求出函数f(x)的图象,然后利用数形结合是解决本题的关键.

练习册系列答案
相关题目
20.《莱茵德纸草书》是世界上最古老的数学著作之一.书中有一道这样的题:把100个面包分给5个人,使每个人的所得成等差数列,且使较大的三份之和的$\frac{1}{7}$是较小的两份之和,则最小一份的量为( )
| A. | $\frac{5}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{6}$ |
4. 执行如图所示的程序框图,输出的s的值为( )
执行如图所示的程序框图,输出的s的值为( )
 执行如图所示的程序框图,输出的s的值为( )
执行如图所示的程序框图,输出的s的值为( )| A. | $\frac{9}{5}$ | B. | $\frac{7}{4}$ | C. | $\frac{11}{6}$ | D. | $\frac{4}{5}$ |
14.在二项式(x-$\frac{1}{x}$)n的展开式中恰好第5项的二项式系数最大,则展开式中含x2项的系数是( )
| A. | 35 | B. | -35 | C. | -56 | D. | 56 |
1.执行如图所示的程序框图,输出的k值为( )


| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
19.在复平面内,复数z=$\frac{2-i}{(1+i)^{2}}$对应的点位于下列哪个象限( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |