题目内容
已知随机变量X服从正态分布N（2，1），且P（1＜x＜3）=0.6826，则P（x＞3）=（ ）
| A、0.1588 |
| B、0.1587 |
| C、0.1586 |
| D、0.1585 |
考点：正态分布曲线的特点及曲线所表示的意义
专题：计算题,概率与统计
分析：根据题目中：“正态分布N（2，1）”，画出其正态密度曲线图：根据对称性，由P（1＜x＜3）=0.6826，可求P（x＞3）．
解答：
解：已知随机变量服从正态分布N（2，1），如图．
∵P（1＜x＜3）=0.6826，
∴P（x＞3）=
（1-0.6826）=0.1587．
故选：B．
解：已知随机变量服从正态分布N（2，1），如图．∵P（1＜x＜3）=0.6826，
∴P（x＞3）=
| 1 |
| 2 |
故选：B．
点评：本题主要考查正态分布曲线的特点及曲线所表示的意义，注意根据正态曲线的对称性解决问题．
练习册系列答案
相关题目
为了了解儿子与其父亲身高的关系，随机抽取5对父子的身高数据如下：
则y关于x的线性回归方程必通过以下哪个点（ ）
| 父亲身高x | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y | 175 | 175 | 176 | 177 | 177 |
| A、（174，175） |
| B、（176，175） |
| C、（174，176） |
| D、（176，176） |
已知a、b、m为正实数，则不等式
＞
成立的条件是（ ）
| a+m |
| b+m |
| a |
| b |
| A、a＜b | B、a＞b |
| C、a≤b | D、a≥b |
有五条线段长度分别为1，3，5，7，9，从这5条线段中任取3条，则所取3条线段能构成一个锐角三角形的概率为（ ）
A、
| ||
B、
| ||
| C、0 | ||
D、
|
已知锐角α，β，满足cosα=
，cos（α+β）=-
，则cosβ=（ ）
| 3 |
| 5 |
| 5 |
| 13 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
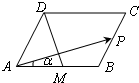在平行四边形ABCD中，AB=2，AD=1，∠DAB=60°，点M为AB的中点，点P从B→C→D（含端点），设∠PAB=α，记tanα=x，
