题目内容
11.以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角”.
该表由若干数字组成,从第二行起,每一行的数字均等于其“肩上”两数之和,表中最后一行今有一个数,则这个数为( )
| A. | 2017×22016 | B. | 2017×22014 | C. | 2016×22017 | D. | 2016×22018 |
分析 数表的每一行都是等差数列,且第一行公差为1,第二行公差为2,第三行公差为4,…,第2015行公差为22014,第2016行只有M,由此可得结论.
解答 解:由题意,数表的每一行都是等差数列,
且第一行公差为1,第二行公差为2,第三行公差为4,…,第2015行公差为22014,
故第1行的第一个数为:2×2-1,
第2行的第一个数为:3×20,
第3行的第一个数为:4×21,
…
第n行的第一个数为:(n+1)×2n-2,
第2016行只有M,
则M=(1+2016)•22014=2017×22014
故选:B.
点评 本题考查了由数表探究数列规律的问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
2.已知三角形ABC的边BC中点为D,且G点满足$\overrightarrow{GA}+\overrightarrow{BG}+\overrightarrow{CG}=\overrightarrow 0$,且$\overrightarrow{AG}=λ\overrightarrow{GD}$,则λ的值是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | $-\frac{1}{2}$ |
19.若$z=\frac{3-i}{1+i}$(其中i是虚数单位),则|z+i|=( )
| A. | $\sqrt{5}$ | B. | $\sqrt{2}$ | C. | 5 | D. | 2 |
3.已知数列{an}的通项${a_n}=2n+3({n∈{N^*}})$,数列{bn}的前n项和为${S_n}=\frac{{3{n^2}+7n}}{2}({n∈{N^*}})$,若这两个数列的公共项顺次构成一个新数列{cn},则满足cm<2012的m的最大整数值为( )
| A. | 335 | B. | 336 | C. | 337 | D. | 338 |
1.若关于x的不等式(ax+1)(ex-aex)≥0在(0,+∞)上恒成立,则实数a的取值范围是( )
| A. | (-∞,1] | B. | [0,1] | C. | $[{0,\frac{e}{2}}]$ | D. | [0,e] |
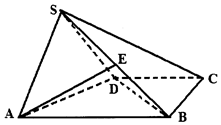 已知四棱锥S-ABCD中,底面是直角梯形,AB=2,BC=CD=1,BC⊥AB,侧面SAD是以∠ASD为直角的等腰三角形,且侧面SAD与底面ABCD垂直.
已知四棱锥S-ABCD中,底面是直角梯形,AB=2,BC=CD=1,BC⊥AB,侧面SAD是以∠ASD为直角的等腰三角形,且侧面SAD与底面ABCD垂直.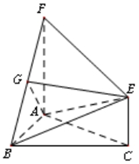 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF∥CE且AF=2CE,G是线段BF上一点,AB=AF=BC=2.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF∥CE且AF=2CE,G是线段BF上一点,AB=AF=BC=2.