题目内容
已知函数f（x）=
+
，
（1）求函数的定义域；
（2）求f（-3），f（
）的值；
（3）当a＞0时，求f（a），f（a-1）的值．
| x+3 |
| 1 |
| x+2 |
（1）求函数的定义域；
（2）求f（-3），f（
| 2 |
| 3 |
（3）当a＞0时，求f（a），f（a-1）的值．
考点：函数的值,函数的定义域及其求法
专题：函数的性质及应用
分析：（1）f（x）=
+
的定义域满足
，由此能求出其定义域．
（2）利用函数性质由解析式求出f（-3），f（
）的值．
（3）利用函数性质由解析式求出f（a），f（a-1）的值．
| x+3 |
| 1 |
| x+2 |
|
（2）利用函数性质由解析式求出f（-3），f（
| 2 |
| 3 |
（3）利用函数性质由解析式求出f（a），f（a-1）的值．
解答：
解：（1）∵f（x）=
+
，
∴函数的定义域满足
，
解得{x|x≥-3，且x≠-2}，
∴函数f（x）=
+
的定义域为{x|x≥-3，且x≠-2}．
（2）∵函数f（x）=
+
，
f(-3)=
+
=-1；
f（
）=
+
=
+
=
+
．
（3）f（a）=
+
；
f（a-1）=
+
=
+
．
| x+3 |
| 1 |
| x+2 |
∴函数的定义域满足
|
解得{x|x≥-3，且x≠-2}，
∴函数f（x）=
| x+3 |
| 1 |
| x+2 |
（2）∵函数f（x）=
| x+3 |
| 1 |
| x+2 |
f(-3)=
| -3+3 |
| 1 |
| -3+2 |
f（
| 2 |
| 3 |
|
| 1 | ||
|
=
|
| 3 |
| 8 |
| ||
| 3 |
| 3 |
| 8 |
（3）f（a）=
| a+3 |
| 1 |
| a+2 |
f（a-1）=
| a-1+3 |
| 1 |
| (a-1)+2 |
=
| a+2 |
| 1 |
| a+1 |
点评：本题考查函数的性质和函数值的求法，是基础题，解题时要注意函数性质的合理运用．
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
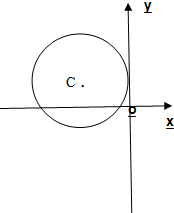如图，已知位于y轴左侧的圆C与y轴相切于点（0，1），且被x轴分成的两段弧长之比为2：1，过点H（0，t）的直线l与圆C相交于M，N两点，且以MN为直径的圆恰好经过坐标原点O．
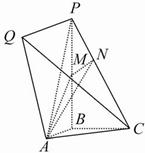如图所示的几何体中，PB⊥平面ABC，PQ∥AB，PQ=PB=1，AB=BC=