题目内容
8.函数f(x)=$\frac{x}{{e}^{|x|}}$的图象大致为( )| A. | 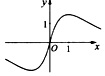 | B. | 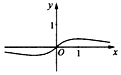 | C. | 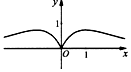 | D. | 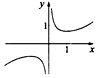 |
分析 利用函数的奇偶性排除选项,然后利用特殊值判断即可.
解答 解:函数f(x)=$\frac{x}{{e}^{|x|}}$,
可得f(-x)=$\frac{-x}{{e}^{|x|}}$=-f(x).
函数是奇函数,排除C;
当x>0时,y=ex与y=x满足ex>x,所以$\frac{x}{{e}^{x}}$<1.
排除A、D;
故选:B.
点评 本题考查函数的图象的判断,函数的奇偶性以及函数的变化趋势,函数的最值,对称性以及周期性往往是判断函数的图象的简洁方法.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
6.矩形纸片ABCD中,AB=10cm,BC=8cm.将其按图(1)的方法分割,并按图(2)的方法焊接成扇形;按图(3)的方法将宽BC 2等分,把图(3)中的每个小矩形按图(1)分割并把4个小扇形焊接成一个大扇形;按图(4)的方法将宽BC 3等分,把图(4)中的每个小矩形按图(1)分割并把6个小扇形焊接成一个大扇形;…;依次将宽BC n等分,每个小矩形按图(1)分割并把2n个小扇形焊接成一个大扇形.当n→∞时,最后拼成的大扇形的圆心角的大小为( )
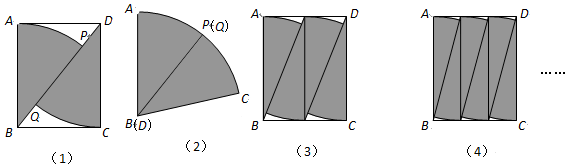

| A. | 小于$\frac{π}{2}$ | B. | 等于$\frac{π}{2}$ | C. | 大于$\frac{π}{2}$ | D. | 大于1.6 |
16.已知在等腰△AOB中,若|OA|=|OB|=5,且$|{\overrightarrow{OA}+\overrightarrow{OB}}|≥\frac{1}{2}|{\overrightarrow{AB}}|$,则$\overrightarrow{OA}•\overrightarrow{OB}$的取值范围是( )
| A. | [-15,25) | B. | [-15,15] | C. | [0,25) | D. | [0,15] |
3.已知全集U=R,集合A={x|ex>1},B={x|x-3>0},则A∩B=( )
| A. | {x|x<3} | B. | {x|x>0} | C. | {x|1<x<3} | D. | {x|0<x<3} |
20.市政府为调查市民对本市某项调控措施的态度,随机抽取了500名市民,统计了他们的月收入频率分布和对该项措施的赞成人数,统计结果如表所示:
(1)从月收入在[60,70)的20人中随机抽取3人,求3人中至少2人对对该措施持赞成态度的概率;
(2)根据用样本估计总体的思想,以样本中事件发生的频率作为相应事件发生的概率,在本市随机采访3人,用X表示3人中对该项措施持赞成态度的人数,求X的分布列和数学期望.
| 月收入(单位:百元) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 25 | 100 | 150 | 155 | 50 | 20 |
| 赞成人数 | 10 | 70 | 120 | 150 | 35 | 15 |
(2)根据用样本估计总体的思想,以样本中事件发生的频率作为相应事件发生的概率,在本市随机采访3人,用X表示3人中对该项措施持赞成态度的人数,求X的分布列和数学期望.
18.已知x,y满足$\left\{\begin{array}{l}{x+y≥4}\\{{x}^{2}+{y}^{2}≤16}\end{array}\right.$,则z=x2+6x+y2+8y+25的取值范围是( )
| A. | [$\frac{121}{2}$,81] | B. | [$\frac{121}{2}$,73] | C. | [65,73] | D. | [65,81] |
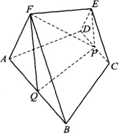 如图,在五面体ABCDEF中,面CDE和面ABF都为等边三角形,面ABCD是等腰梯形,点P、Q分别是CD、AB的中点,FQ∥EP,PF=PQ,AB=2CD=2.
如图,在五面体ABCDEF中,面CDE和面ABF都为等边三角形,面ABCD是等腰梯形,点P、Q分别是CD、AB的中点,FQ∥EP,PF=PQ,AB=2CD=2.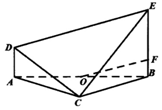 如图,在以A、B、C、D、E为顶点的五面体中,AD⊥平面ABC,AD∥BE,AC⊥CB,AB=2BE=4AD=4.
如图,在以A、B、C、D、E为顶点的五面体中,AD⊥平面ABC,AD∥BE,AC⊥CB,AB=2BE=4AD=4.