题目内容
(1)已知抛物线过点A(1,2),求抛物线的标准方程;
(2)已知双曲线的一个焦点与抛物线y2=8x的焦点重合,且双曲线的离心率等于2,求双曲线的标准方程.
(2)已知双曲线的一个焦点与抛物线y2=8x的焦点重合,且双曲线的离心率等于2,求双曲线的标准方程.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)先根据点的位置确定抛物线焦点的位置,然后分焦点在x轴的正半轴时、焦点在y轴的正半轴时两种情况进行求解;
(2)确定双曲线的一个焦点为(2,0),即c=2,利用双曲线的离心率等于2,可得a=1,求出b,即可求出双曲线的标准方程.
(2)确定双曲线的一个焦点为(2,0),即c=2,利用双曲线的离心率等于2,可得a=1,求出b,即可求出双曲线的标准方程.
解答:
解:(1)点M(1,2)是第一象限的点
当抛物线的焦点在x轴的正半轴时,设抛物线的方程为y2=2px(p>0)
∴4=2p,p=2,即抛物线的方程是y2=4x;
当抛物线的焦点在y轴的正半轴时,设抛物线的方程为x2=2py(p>0)
∴1=4p,p=
,即抛物线的方程是x2=
y.
故抛物线的标准方程为x2=
y,或y2=4x
(2)抛物线y2=8x的焦点为(2,0),
∵双曲线的一个焦点与抛物线y2=8x的焦点重合,
∴双曲线的一个焦点为(2,0),即c=2,
∵双曲线的离心率等于2,
∴a=1,
∴b=
,
∴双曲线的标准方程为x2-
=1
当抛物线的焦点在x轴的正半轴时,设抛物线的方程为y2=2px(p>0)
∴4=2p,p=2,即抛物线的方程是y2=4x;
当抛物线的焦点在y轴的正半轴时,设抛物线的方程为x2=2py(p>0)
∴1=4p,p=
| 1 |
| 4 |
| 1 |
| 2 |
故抛物线的标准方程为x2=
| 1 |
| 2 |
(2)抛物线y2=8x的焦点为(2,0),
∵双曲线的一个焦点与抛物线y2=8x的焦点重合,
∴双曲线的一个焦点为(2,0),即c=2,
∵双曲线的离心率等于2,
∴a=1,
∴b=
| 3 |
∴双曲线的标准方程为x2-
| y2 |
| 3 |
点评:本题主要考查了抛物线的简单性质,考查抛物线、双曲线的方程.(1)注意讨论焦点在x轴和y轴两种情况.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
下列函数与函数y=x相等的是( )
| A、y=logaax(a>0,a≠1) | ||
B、y=
| ||
C、y=
| ||
D、y=(
|
若实数x,y满足
,则z=y-x的最小值为( )
|
| A、8 | B、-8 | C、-6 | D、6 |
如图,在正方体ABCD-A1B1C1D1中,AC与A1D所在直线所成的角等于( )
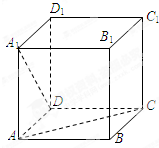

| A、30° | B、45° |
| C、60° | D、90° |
一块电路板的AB线段之间有60个串联的焊接点,知道电路不通的原因是焊口脱落造成的.要想用二分法的思想检测出哪处焊口脱落.至少需要检测( )
| A、4次 | B、6次 | C、8次 | D、30次 |
若直线a与平面α垂直,那么平面α与直线a平行的直线有( )
| A、0条 | B、0条或无数条 |
| C、无数条 | D、不确定 |
平面向量
,
的夹角为60°,
=(2,0),|
|=1,则|
+2
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
A、2
| ||||
B、
| ||||
C、
| ||||
| D、2 |
函数y=log
(x-3)的定义域为( )
| 1 |
| 2 |
| A、(3,+∞) |
| B、[3,+∞) |
| C、(-∞,3) |
| D、(-∞,3] |