题目内容
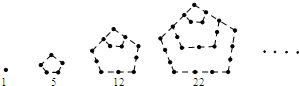
如图实心点的个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作a1=1,第2个五角形数记作
a2=5,第3个五角形数记作a3=12,第4个五角形数记作a4=22,…,若按此规律继续下去,若an=145,则n= .
a2=5,第3个五角形数记作a3=12,第4个五角形数记作a4=22,…,若按此规律继续下去,若an=145,则n=

考点:归纳推理
专题:推理和证明
分析:根据题目所给出的五角形数的前几项,发现该数列的特点是,从第二项起,每一个数与前一个数的差构成了一个新的等差数列,写出对应的n-1个等式,然后用累加的办法求出该数列的通项公式,然后代入项求项数.
解答:
解:a2-a1=5-1=4,a3-a2=12-5=7,a4-a3=22-12=10,…,由此可知数列{an+1-an}构成以4为首项,以3为公差的等差数列.
所以an+1-an=4+3(n-1)=3n+1.
a2-a1=3×1+1
a3-a2=3×2+1
…
an-an-1=3(n-1)+1
累加得:an-a1=3(1+2+…+(n-1))+n-1
所以an=a1+3×
+n-1=1+
+n-1=
.
由an=
=145,解得:n=-
(舍),或n=10.
故答案为:10.
所以an+1-an=4+3(n-1)=3n+1.
a2-a1=3×1+1
a3-a2=3×2+1
…
an-an-1=3(n-1)+1
累加得:an-a1=3(1+2+…+(n-1))+n-1
所以an=a1+3×
| n(n-1) |
| 2 |
| 3n(n-1) |
| 2 |
| 3n2-n |
| 2 |
由an=
| 3n2-n |
| 2 |
| 29 |
| 3 |
故答案为:10.
点评:本题考查了等差数列的通项公式,解答此题的关键是能够由数列的前几项分析出数列的特点,即从第二项起,每一个数与前一个数的差构成了一个新的等差数列,本题训练了一种求数列通项的重要方法--累加法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
三个数(
)-
,(
)-
,(
)-
的大小顺序是( )
| 2 |
| 5 |
| 1 |
| 5 |
| 6 |
| 5 |
| 1 |
| 5 |
| 6 |
| 5 |
| 2 |
| 5 |
A、(
| ||||||||||||
B、(
| ||||||||||||
C、(
| ||||||||||||
D、(
|
设偶函数f(x)的定义域为R,当x∈(-∞,0]是减函数,则f(-2),f(-3),f(π)的大小关系是( )
| A、f(π)>f(-3)>f(-2) |
| B、f(π)>f(-2)>f(-3) |
| C、f(-2)>f(-3)>f(π) |
| D、f(-3)>f(-2)>f(π) |
不等式
≥0的解集为( )
| 1-x |
| 2x+1 |
A、(-
| ||
B、[-
| ||
C、(-∞,-
| ||
D、(-∞,-
|