题目内容
在DABC中,角A、B、C的对边分别为 ,且4bsinA=
,且4bsinA=
 .
.
(I)求sinB的值;
(II)若 成等差数列,且公差大于0,求cosA-cosC的值.
成等差数列,且公差大于0,求cosA-cosC的值.
(Ⅰ)由4bsinA= a,根据正弦定理得4sinBsinA=
a,根据正弦定理得4sinBsinA= sinA,
sinA,
所以sinB= .
.
(Ⅱ)由已知和正弦定理以及(Ⅰ)得
sinA+sinC= . ①
. ①
设cosA-cosC=x, ②
①2+②2,得2-2cos(A+C)= +x2. ③
+x2. ③
又a<b<c,A<B<C,所以0°<B<90°,cosA>cosC,
故cos(A+C)=-cosB=- .
.
代入③式得x2= .
.
因此cosA-cosC= .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,直线
中,直线 是曲线
是曲线 的切线,则当
的切线,则当 >0时,实数
>0时,实数 的最小值是 .
的最小值是 . 中,已知
中,已知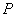 是函数
是函数 的图象上的动点,该图象
的图象上的动点,该图象 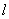 交
交 轴于点
轴于点 ,过点
,过点 .
.  的范围是
的范围是 B.
B.  C.
C.  D.
D. 

 的前n项和Sn ,且
的前n项和Sn ,且
 B.
B. C
C  D.
D.
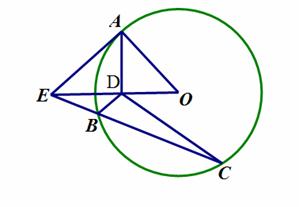
 中,
中, ,则数列
,则数列 ;
; ,试求
,试求 的大小.
的大小.
 满足:集合
满足:集合 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数 ;②
;② ;③
;③ 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明) 是否为等比源函数,并证明你的结论;
是否为等比源函数,并证明你的结论; ,函数
,函数 都是等比源函数.
都是等比源函数.