题目内容
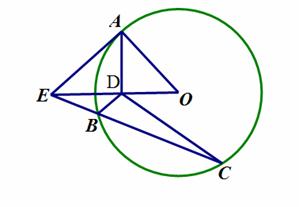
如图,AE是圆O的切线,A是切点,AD⊥OE于D, 割线EC交圆O于B、C两点.
(Ⅰ)证明:O,D,B,C四点共圆;
(Ⅱ)设∠DBC=50°,∠ODC=30°,求∠OEC的大小.
解:
(Ⅰ)连结OA,则OA⊥EA.由射影定理得EA2=ED·EO.
由切割线定理得EA2=EB·EC,故ED·EO=EB·EC,即 =
= ,
,
又∠OEC=∠OEC,所以△BDE∽△OCE,所以∠EDB=∠OCE.
因此O,D,B,C四点共圆.


(Ⅱ)连结OB.因为∠OEC+∠OCB+∠COE=180°,结合(Ⅰ)得
∠OEC=180°-∠OCB-∠COE=180°-∠OBC-∠DBE
=180°-∠OBC-(180°-∠DBC)=∠DBC-∠ODC=20°.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 ,
, (
( 为虚数单位).在复平面内,
为虚数单位).在复平面内, 对应的点在第 象限.
对应的点在第 象限. 满足
满足 ,等比数列
,等比数列 满足.
满足. .
. (II)设
(II)设 ,求数列
,求数列 的前
的前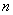 项和
项和 .
. 左支上一点P
左支上一点P 到直线
到直线 =x的距离
=x的距离 , 则
, 则
 ,且4bsinA=
,且4bsinA=
 .
. :“若直线
:“若直线 与直线
与直线 垂直,则
垂直,则 ”;
”;
 :“
:“ 是
是 的充要条件”,则( )
的充要条件”,则( ) 真 B.
真 B. 真 C.
真 C. 真 D.
真 D. 假
假 轴正半轴上一点
轴正半轴上一点 ,作圆
,作圆 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,则
,则 的最小值为( )
的最小值为( ) C.2 D.3
C.2 D.3 满足
满足 ,则
,则 的最小值为
的最小值为  B.
B. 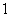 C.
C.  D.
D. 