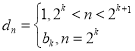Question

【题目】如图，在直四棱柱ABCD﹣A1B1C1D1中，底面ABCD为菱形，∠ABC＝60°，AA1AB，M，N分别为AB，AA1的中点.

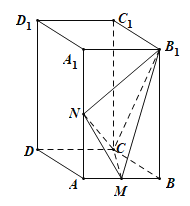
（1）求证：平面B1NC⊥平面CMN；

（2）若AB＝2，求点N到平面B1MC的距离.

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）推导出AA1⊥平面ABCD，AA1⊥CM，CM⊥AB，从而CM⊥平面ABB1A1，进而CM⊥B1N，推导出△A1B1N∽△ANM，从而∠A1B1N＝∠ANM，∠A1NB1＝∠AMN，进而B1N⊥MN，B1N⊥平面CMN，由此能证明平面B1NC⊥平面CMN.

（2）求出点B1到平面CMN的距离为h1，设N到平面B1CM的距离为h2，由，能求出点N到平面B1MC的距离.

（1）证明：∵直四棱柱ABCD﹣A1B1C1D1，∴AA1⊥平面ABCD，

∵CM平面ABCD，∴AA1⊥CM，

∵底面ABCD是菱形，∠ABC＝60°，M是AB的中点，

∴CM⊥AB，

∵AA1∩AB＝A，AA1平面ABB1A1，AB平面ABB1A1，

∴CM⊥平面ABB1A1，

∵B1N平面ABB1A1，∴CM⊥B1N，

∵M是AB中点，N为AA1中点，AA1，

∴，，

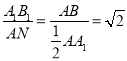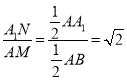∵∠B1A1N＝∠NAM＝90°，∴△A1B1N∽△ANM，

∴∠A1B1N＝∠ANM，∠A1NB1＝∠AMN，

∴∠A1NB1+∠ANM＝90°，∴B1N⊥MN，

∵MN∩CM＝M，∴B1N⊥平面CMN，

∵B1N平面B1NC，∴平面B1NC⊥平面CMN.

（2）∵在直四棱柱ABCD﹣A1B1C1D1中，底面ABCD为菱形，∠ABC＝60°，

AA1AB，AB＝2，M，N分别为AB，AA1的中点.

∴MN，B1M3，B1C，

BN，

∵底面ABCD是菱形，∠ABC＝60°，

∴CM，CN，

由（1）知B1N⊥平面CMN，设点B1到平面CMN的距离为h1，h1，

∵CN2＝MN2+CM2，∴，

∴，

∵B1M＝3，，∴，

设N到平面B1CM的距离为h2，

∵，

∴，

解得h2.

∴点N到平面B1MC的距离为.