题目内容
【题目】已知![]() 为坐标原点,
为坐标原点,![]() 为坐标平面内动点,且
为坐标平面内动点,且![]() 成等差数列.
成等差数列.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 作直线交
作直线交![]() 于
于![]() 两点(不与原点重合),是否存在
两点(不与原点重合),是否存在![]() 轴上一定点
轴上一定点![]() ,使得_________.若存在,求出定点
,使得_________.若存在,求出定点![]() ,若不存在,说明理由.从“①作
,若不存在,说明理由.从“①作![]() 点关于
点关于![]() 轴的对称点
轴的对称点![]() ,则
,则![]() 三点共线;②
三点共线;②![]() ”这两个条件中选一个,补充在上面的问题中并作答(注:如果选择两个条件分别作答,按第一个解答计分)
”这两个条件中选一个,补充在上面的问题中并作答(注:如果选择两个条件分别作答,按第一个解答计分)
【答案】(1)![]() ;(2)两种选择都存在
;(2)两种选择都存在![]() 满足条件.
满足条件.
【解析】
(1)设![]() ,
,![]() ,
,![]() ,由已知得关于
,由已知得关于![]() ,
,![]() 的关系式,整理即可求得点
的关系式,整理即可求得点![]() 的轨迹方程;
的轨迹方程;
(2)当选①时,设![]() ,与
,与![]() 联立,得关于
联立,得关于![]() 的一元二次方程,利用根与系数的关系可得
的一元二次方程,利用根与系数的关系可得![]() ,
,![]() 横坐标的和与积,写出直线
横坐标的和与积,写出直线![]() 的方程,由直线系方程可得,直线
的方程,由直线系方程可得,直线![]() 过定点
过定点![]() ,说明结论成立;
,说明结论成立;
当选②时,假设存在![]() 满足条件②,设
满足条件②,设![]() ,与
,与![]() 联立,得关于
联立,得关于![]() 的一元二次方程,利用根与系数的关系可得
的一元二次方程,利用根与系数的关系可得![]() ,
,![]() 横坐标的和与积,由
横坐标的和与积,由![]() 求得
求得![]() ,说明存在
,说明存在![]() 满足条件.
满足条件.
解:(1)设![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
由2,![]() ,
,![]() 成等差数列,得
成等差数列,得![]() ,即
,即![]() ,
,
即![]() ,化简得
,化简得![]() ,
,
![]() 点
点![]() 的轨迹方程为
的轨迹方程为![]() ;
;
(2)当选①时,设![]() ,与
,与![]() 联立,得
联立,得![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
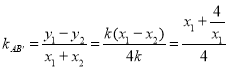 ,
,
![]() ,化简得
,化简得![]() ,
,
![]() 存在
存在![]() 满足条件.
满足条件.
当选②时,假设存在![]() 满足条件②,
满足条件②,
设![]() ,与
,与![]() 联立,得
联立,得![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,即
,即![]() ,
,
![]() 存在
存在![]() 满足条件.
满足条件.

练习册系列答案
相关题目