题目内容
16.若θ是第二象限角,且$cos\frac{θ}{2}-sin\frac{θ}{2}=\sqrt{1-sinθ}$,则$\frac{θ}{2}$是( )| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
分析 根据$cos\frac{θ}{2}-sin\frac{θ}{2}=\sqrt{1-sinθ}$,可得$cos\frac{θ}{2}≥sin\frac{θ}{2}$,θ是第二象限角,即可判断$\frac{θ}{2}$.
解答 解:由题意,∵$cos\frac{θ}{2}-sin\frac{θ}{2}=\sqrt{1-sinθ}$,
∴$cos\frac{θ}{2}≥sin\frac{θ}{2}$,
∵θ是第二象限角,
∴$\frac{θ}{2}$在第一、三象限角.
得$\frac{θ}{2}$是在三象限角.
故选C.
点评 本题主要考查了象限角的判断.属于基础题.

练习册系列答案
相关题目
9.在一次期末数学测试中,唐老师任教班级学生的考试得分情况如表所示:
(1)根据上述表格,试估计唐老师所任教班级的学生在本次期末数学测试的平均成绩;
(2)若学生的成绩大于或等于130分为优秀,小于130分且大于等于90分为合格,小于90分为不及格,若是优秀,学生在期末综合测评中可得到40分,若是合格,学生在期末综合测评中可得到20分,若是不合格,学生在期末综合测评中则扣20分,以频率估计概率,若从大量的学生中随机抽取2人,这2人在数学科目的期末综合测评分数之和记为X,求X的分布列和数学期望.
| 分数区间 | [50,70] | [70,90] | [90,110] | [110,130] | [130,150] |
| 人数 | 2 | 8 | 32 | 38 | 20 |
(2)若学生的成绩大于或等于130分为优秀,小于130分且大于等于90分为合格,小于90分为不及格,若是优秀,学生在期末综合测评中可得到40分,若是合格,学生在期末综合测评中可得到20分,若是不合格,学生在期末综合测评中则扣20分,以频率估计概率,若从大量的学生中随机抽取2人,这2人在数学科目的期末综合测评分数之和记为X,求X的分布列和数学期望.
8.从编号为01,02,…,49,50的50个个体中利用下面的随机数表选取5个个体,选取方法从随机数表第1行第5列的数开始由左到右依次抽取,则选出来的第5个个体的编号为( )


| A. | 14 | B. | 07 | C. | 32 | D. | 43 |
1.函数f(x)=6+4x-x4在[-1,2]上的最大值和最小值分别为( )
| A. | f(1)和f(2) | B. | f(1)和f(-1) | C. | f(-1)和f(2) | D. | f(2)和f(-1) |
4.已知圆的半径为πcm,则120°的圆心角所对的弧长是( )
| A. | $\frac{π}{3}$cm | B. | $\frac{{π}^{2}}{3}$cm | C. | $\frac{2π}{3}$cm | D. | $\frac{2{π}^{2}}{3}$cm |
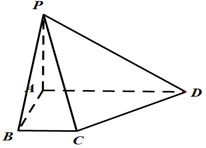 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,AD=3BC.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,AD=3BC.