题目内容
12.已知数列{an}中a1=3,其前n项和Sn满足Sn=$\frac{1}{2}$an+1-$\frac{3}{2}$.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设{bn}是公差为3的等差数列,b1=1.现将数列{an}中的a${\;}_{{b}_{1}}$,a${\;}_{{b}_{2}}$,…a${\;}_{{b}_{n}}$…抽出,按原有顺序组成一新数列{cn},试求数列{cn}的前n项和Tn.
分析 (I)利用递推关系与等比数列的通项公式即可得出;
(II)bn=b1+(n-1)d=3n-2,可得${c_n}={a_{b_n}}={a_{3n-2}}={3^{3n-2}}$,再利用等比数列的前n项和公式即可得出.
解答 解:(Ⅰ)当n=1时,${S_1}={a_1}=\frac{1}{2}{a_2}-\frac{3}{2}=3$,∴a2=9 (2分)
∵${S_n}=\frac{1}{2}•{a_{n+1}}-\frac{3}{2}$,
∴${S_{n-1}}=\frac{1}{2}•{a_n}-\frac{3}{2},\;(n≥2)$,
相减得:$\frac{{{a_{n+1}}}}{a_n}=3\;(n≥2)$,
∴an=${a}_{2}•{3}^{n-2}$=3n,(5分)
当n=1时,符合${a_n}={3^n}$,(6分)
∴${a_n}={3^n}$. (7分)
(Ⅱ)bn=b1+(n-1)d=3n-2,(9分)
${c_n}={a_{b_n}}={a_{3n-2}}={3^{3n-2}}$ (12分)
∴{cn}是以3为首项,以27为公比的等比数列,
∴${T_n}=\frac{{3(1-{{27}^n})}}{1-27}=\frac{3}{26}({27^n}-1)$ (15分)
点评 本题考查了递推关系、等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.过点(-1,0)与抛物线y=x2-1只有一个公共点的直线有( )
| A. | 3条 | B. | 2条 | C. | 1条 | D. | 0条 |
3.函数y=sinx的最小正周期是( )
| A. | π | B. | 2π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
7.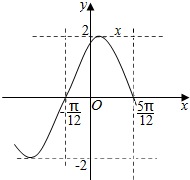 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )
 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )| A. | $\sqrt{3}$ | B. | 0 | C. | -2 | D. | 1 |
17.在△ABC中,已知D是BC延长线上一点,若$\overrightarrow{BC}$=2$\overrightarrow{CD}$,点E为线段AD的中点,$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+$\frac{3}{4}\overrightarrow{AC}$,则λ=( )
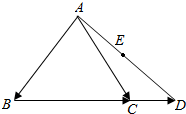

| A. | $\frac{1}{4}$ | B. | $-\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
1.一个直四棱柱的侧棱长等于2,底面是边长为1的正方形,如果其俯视图是一个面积为1的正方形,其侧视图的面积的取值范围是( )
| A. | [1,2] | B. | [2,2$\sqrt{2}$] | C. | [1,2$\sqrt{2}$] | D. | [$\sqrt{3}$,2$\sqrt{2}$] |