题目内容
17.在区间[-1,1]上任取两数m和n,则关于x的方程x2+mx+n=0的两根都是负数的概率( )| A. | $\frac{1}{48}$ | B. | $\frac{1}{24}$ | C. | $\frac{13}{24}$ | D. | $\frac{11}{24}$ |
分析 根据几何概型的概率公式,利用积分求出对应区域的面积进行求解即可.
解答 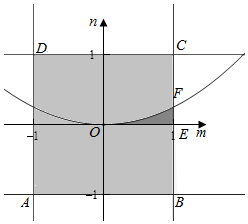 解:∵区间[-1,1]上任取两数m和n,∴$\left\{\begin{array}{l}{-1≤m≤1}\\{-1≤n≤1}\end{array}\right.$,对应的区域为正方形,面积S=2×2=4,
解:∵区间[-1,1]上任取两数m和n,∴$\left\{\begin{array}{l}{-1≤m≤1}\\{-1≤n≤1}\end{array}\right.$,对应的区域为正方形,面积S=2×2=4,
若方程x2+mx+n=0的两根都是负数,
则$\left\{\begin{array}{l}{△={m}^{2}-4n≥0}\\{{x}_{1}{x}_{2}=n>0}\\{{x}_{1}+{x}_{2}=-m<0}\end{array}\right.$,即$\left\{\begin{array}{l}{n<\frac{{m}^{2}}{4}}\\{n>0}\\{m>0}\end{array}\right.$,
作出不等式组对应的平面区域如图:
则对应的面积S=∫${\;}_{0}^{1}$$\frac{{m}^{2}}{4}$dm=$\frac{1}{12}$m3|${\;}_{0}^{1}$=$\frac{1}{12}$,
则对应的概率P=$\frac{\frac{1}{12}}{4}$=$\frac{1}{48}$,
故选:A.
点评 本题主要考查几何概型的概率的计算,根据条件求出对应的区域以及区域的面积是解决本题的关键.

练习册系列答案
相关题目
8.设实数p在[0,5]上随机地取值,使方程x2+px+1=0有实根的概率为( )
| A. | 0.6 | B. | 0.5 | C. | 0.4 | D. | 0.3 |
5.在等差数列{an}中,a4=2,且a1+a2+…+a10=65,则公差d的值是( )
| A. | 4 | B. | 3 | C. | 1 | D. | 2 |
12.在区间[0,π]上随机地取一个数x,则事件“sinx≤$\frac{1}{2}$”发生的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
2.已知等差数列{an}的前n项和为Sn,公差为d,若$\frac{{S}_{2016}}{2016}$-$\frac{{S}_{16}}{16}$=100,则d的值为( )
| A. | $\frac{1}{20}$ | B. | $\frac{1}{10}$ | C. | 10 | D. | 20 |
6.定义在R上的偶函数f(x)满足:f(x+1)=f(x-1),若f(x)在区间[0,1]内单调递增,则f(-$\frac{3}{2}$)、f(1)、f($\frac{4}{3}$)的大小关系为( )
| A. | f(-$\frac{3}{2}$)<f(1)<f($\frac{4}{3}$) | B. | f(1)<f(-$\frac{3}{2}$)<f($\frac{4}{3}$) | C. | f(-$\frac{3}{2}$)<f($\frac{4}{3}$)<f(1) | D. | f($\frac{4}{3}$)<f(1)<f(-$\frac{3}{2}$) |
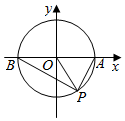 如图,在平面直角坐标系xOy中,单位圆与x轴的正半轴与负半轴分别交于点A,B,角α的始边为OA,终边与单位圆交于x轴下方一点P.
如图,在平面直角坐标系xOy中,单位圆与x轴的正半轴与负半轴分别交于点A,B,角α的始边为OA,终边与单位圆交于x轴下方一点P.