题目内容
已知函数y=f（x）在R上为偶函数，当x≥0时，f（x）=log3（x+1），若f（t）＞f（2-t），则实数t的取值范围是 ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据函数的奇偶性将不等式转化为 f（|t|）＞f（|2-t|）．利用函数的单调性解不等式即可得到结论．
解答：
解：由于函数y=f（x）的图象关于y轴对称，且在x≥0上为增函数，
∴不等式 f（t）＞f（2-t）等价为 f（|t|）＞f（|2-t|），
即|t|＞|2-t|，由此解得t＞1，
∴t的取值范围是（1，+∞）．
故答案为：（1，+∞）．
∴不等式 f（t）＞f（2-t）等价为 f（|t|）＞f（|2-t|），
即|t|＞|2-t|，由此解得t＞1，
∴t的取值范围是（1，+∞）．
故答案为：（1，+∞）．
点评：本题主要考查不等式的解法，利用函数的奇偶性和单调性之间的关系，将不等式进行等价转化是解决本题的关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
执行如图所示的程序框图，若输入的x的值为3，则输出的y的值为（ ）
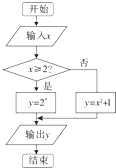
| A、4 | B、5 | C、8 | D、10 |
将函数y=sin（2x-θ）的图象F向右平移
个单位长度得到图象F′，若F′的一个对称中心是（
π，0），则θ的一个可能取值是（ ）
| π |
| 6 |
| 3 |
| 8 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|