题目内容

13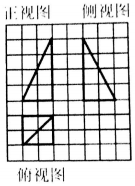．如图所示，网格纸上小正方形的边长为1，粗线画出的是某一几何体的三视图，则该几何体外接球的表面积为（　　）
A．8πB．16πC．20πD．24π

分析 根据三视图可知该几何体为四棱锥，且四棱锥的一条侧棱与底面垂直，把四棱锥补成长方体，则长方体的长宽高分别为2，2，4，利用CFT 的对角线为外接球的直径求外接球的半径，代入球的表面积公式计算．

解答 解：由三视图知：几何体为四棱锥，且四棱锥的一条侧棱与底面垂直，
把四棱锥补成长方体，则长方体的长宽高分别为2，2，4，
∴长方体的外接球就是四棱锥的外接球，
∴外接球的直径2R=$\sqrt{4+4+16}$=2$\sqrt{6}$，∴R=$\sqrt{6}$，
∴外接球的表面积S=4πR2=4π×6=24π．
故选D．

点评 本题考查了由三视图求几何体的外接球的表面积，判断几何体的几何特征，是解决本题的关键．

练习册系列答案
相关题目
3．设数列{an}是单调递增的等差数列，a1=2且a1-1，a3，a5+5成等比数列，则a2017=（　　）
A．1008B．1010C．2016D．2017
4．我们可以利用数列{an}的递推公式an=$\left\{\begin{array}{l}{n，n为奇数时}\\{\frac{{a}_{n}}{2}，n为偶数时}\end{array}\right.$（n∈N+），求出这个数列各项的值，使得这个数列中的每一项都是奇数，则a64+a65=66．
1．已知数列{an}为等差数列，a1=1，an＞0，其前n项和为Sn，且数列$\left\{{\sqrt{S_n}}\right\}$也为等差数列，设bn=$\frac{{a}_{n+2}}{{2}^{n}•{a}_{n}•{a}_{n+1}}$，则数列{bn}的前n项和Tn=1-$\frac{1}{{2}^{n}•（2n+1）}$．
8．已知集合M={x|x2-2x-3≤0}，N={x|log2x＞1}，则M∩N=（　　）
A．[-1，2）B．[-1，+∞）C．（2，3]D．（2，+∞）
18．已知数列{an}为等差数列，a1=1，an＞0，其前n项和为Sn，且数列{$\sqrt{{S}_{n}}$}也为等差数列．．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=$\frac{{a}_{n+1}}{{S}_{n}•{S}_{n+1}}$，求数列{bn}的前n项和．
5．设函数f（x）=alnx-bx2．
（1）当b=1时，讨论函数f（x）的单调性；   
（2）当a=1，b=0时，函数g（x）=f（x）-kx，k为常数，若函数g（x）有两个相异零点x1，x2，证明：x1•x2＞e2．
2．过抛物线y2=2px（p＞0）焦点F的直线与双曲线x2-$\frac{{y}^{2}}{8}$=1的一条渐近线平行，并交其抛物线于A，B两点，若|AF|＞|BF|，且|AF|=3，则抛物线方程为（　　）
A．y2=xB．y2=2xC．y2=4xD．y2=8x
2．已知α、β∈（0，π），且tanα、tanβ是方程x2-5x+6=0的两根，试求：
（1）α+β的值；
（2）tan2（α+β）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网