题目内容
已知函数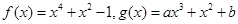 (
(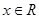 ),其中
),其中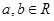 .
.
(1)若曲线 与
与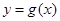 在点
在点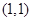 处相交且有相同的切线,求
处相交且有相同的切线,求 的值;
的值;
(2)设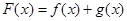 ,若对于任意的
,若对于任意的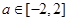 ,函数
,函数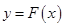 在区间
在区间 上的值恒为负数,求
上的值恒为负数,求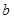 的取值范围.
的取值范围.
(1)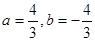 ;(2)
;(2)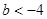
解析试题分析:(1)确定 的值,需要确定两个独立的条件,依题意,首先
的值,需要确定两个独立的条件,依题意,首先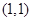 在曲线
在曲线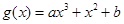 上,代入得关于
上,代入得关于 的方程,再
的方程,再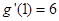 ,又得关于
,又得关于 的方程,联立求
的方程,联立求 ;(2)多元函数,可采取选取主元法.由题意知,对任意的
;(2)多元函数,可采取选取主元法.由题意知,对任意的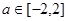 ,在
,在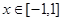 上
上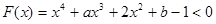 恒成立,首先采取参变分离法,变形为
恒成立,首先采取参变分离法,变形为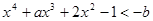 恒成立,左边看作自变量为
恒成立,左边看作自变量为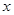 的函数
的函数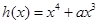
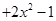 ,
,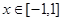 ,只需求函数
,只需求函数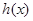 的最大值,且
的最大值,且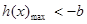 .
.
试题解析:(1) ,切线斜率
,切线斜率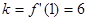 ,
,
由题知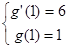 ,即
,即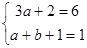 ,解得
,解得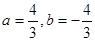 .
.
(2)由题知对任意的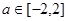 ,在
,在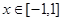 上
上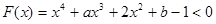 恒成立,
恒成立,
即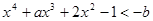 恒成立.
恒成立.
设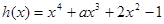 ,则
,则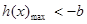
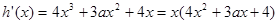 ,
,
令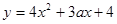 ,则对任意的
,则对任意的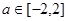 ,恒有
,恒有 ,则恒有
,则恒有
当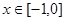 时,
时,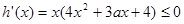 ,函数
,函数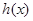 单调递减,
单调递减,
当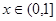 时,
时, ,函数
,函数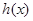 单调递增。
单调递增。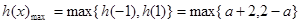 =4,
=4,
所以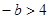 ,即
,即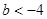
考点:1、导数的几何意义;2、利用导数求函数的极值、最值.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
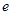 是自然对数的底数,函数
是自然对数的底数,函数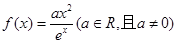 .
. 的单调递增区间;
的单调递增区间;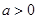 时,函数
时,函数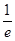 ,求
,求 的值.
的值.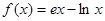 ,
, 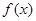 的单调区间;
的单调区间;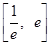 内存在
内存在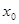 ,使不等式
,使不等式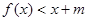 成立,求
成立,求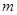 的取值范围.
的取值范围. (如图所示,其中O为圆心,
(如图所示,其中O为圆心,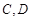 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).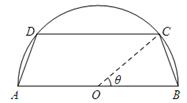
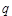 的值,使体积V最大;
的值,使体积V最大;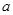 为实数,函数
为实数,函数 .
. 的单调区间与极值;
的单调区间与极值;  且
且 时,
时, .
.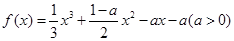 .
.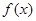 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;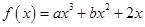 在
在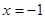 处取得极值,且在点
处取得极值,且在点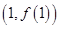 处的切线斜率为
处的切线斜率为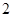 .
.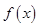 的单调增区间;
的单调增区间; 的方程
的方程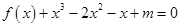 在区间
在区间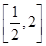 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数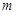 的取值范围.
的取值范围.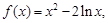
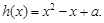
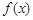 的极值;
的极值;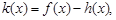 若函数
若函数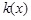 在
在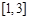 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数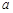 的取值范围.
的取值范围.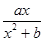 ,且f(x)的图象在x=1处与直线y=2相切.
,且f(x)的图象在x=1处与直线y=2相切.