题目内容
5.函数y=sinx与y=cosx在x∈[0,$\frac{π}{2}$]内的交点为P,在点P处两函数的切线与x轴所围成的三角形的面积为$\frac{\sqrt{2}}{2}$.分析 联立y=sinx与y=cosx求出在[0,$\frac{π}{2}$]内的交点P坐标,然后求出该点处两切线方程,从而求出三角形的三个顶点坐标,最后根据三角形面积公式求解.
解答 解:由sinx=cosx,且x∈[0,$\frac{π}{2}$],得x=$\frac{π}{4}$,
∴y=sinx与y=cosx在[0,$\frac{π}{2}$]内的交点P的坐标是($\frac{π}{4}$,$\frac{\sqrt{2}}{2}$),
函数y=sinx与y=cosx的导函数分别为y=cosx与y=-sinx,
则两函数在($\frac{π}{4}$,$\frac{\sqrt{2}}{2}$)处的切线的斜率分别为$\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}$.
得两条切线方程分别是y-$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$(x-$\frac{π}{4}$)和y-$\frac{\sqrt{2}}{2}$=-$\frac{\sqrt{2}}{2}$(x-$\frac{π}{4}$),
y=0时,x=$\frac{π}{4}$-1,x=$\frac{π}{4}$+1,
于是三角形三顶点坐标分别为($\frac{π}{4}$,$\frac{\sqrt{2}}{2}$),($\frac{π}{4}$-1,0),($\frac{π}{4}$+1,0),
S=$\frac{1}{2}$×2×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$,
即它们与x轴所围成的三角形的面积是$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题主要考查了利用导数研究函数的再某点切线方程,以及三角方程和三角形面积公式,属于中档题.

| x | 197 | 198 | 201 | 204 | 205 |
| y | 1 | 3 | 6 | 7 | m |
| x | 3.5 | 4.5 | 5.5 | 6.5 |
| y | 3 | 4m | 4 | 5 |
| A. | 1 | B. | 0.85 | C. | 0.95 | D. | 0.9 |
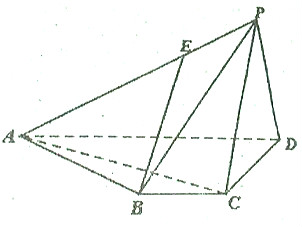 如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.
如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.