题目内容
5.已知函数f(x)=ln(1+x)-x-ax2,a∈R.(Ⅰ)若函数f(x)在区间$[{-\frac{1}{2},-\frac{1}{3}}]$上有单调递增区间,求实数a的取值范围;
(Ⅱ)证明不等式:$\frac{1}{ln2}+\frac{1}{ln3}+…+\frac{1}{ln(n+1)}>\frac{n}{n+1}$.
分析 (Ⅰ)由题知f(x)的定义域为(-1,+∞),求出函数的导函数,可得当a=0时,f′(x)>0在$[{-\frac{1}{2},-\frac{1}{3}}]$上恒成立;当a≠0时,求出导函数的两个零点,分a>0和a<0讨论求得使函数f(x)在$[{-\frac{1}{2},-\frac{1}{3}}]$上有单调递增区间的a的范围;
(Ⅱ)取a=1,可知在(0,+∞)上,f′(x)<0恒成立,即函数f(x)在区间(0,+∞)上单调递减,由此得到ln(1+x)<x+x2在区间(0,+∞)上恒成立,
取x=n,n∈N*,则0<ln(1+n)<n+n2,得$\frac{1}{ln(1+n)}>\frac{1}{{n+{n^2}}}$=$\frac{1}{n}-\frac{1}{n+1}$,分别取n=1,2,3,…,n,利用累加法证明$\frac{1}{ln2}+\frac{1}{ln3}+…+\frac{1}{ln(n+1)}>\frac{n}{n+1}$.
解答 解:(Ⅰ)由题知f(x)的定义域为(-1,+∞),
${f^'}(x)=\frac{1}{x+1}-1-2ax=\frac{{-2a{x^2}-(2a+1)x}}{x+1}$,
当a=0时,${f^'}(x)=\frac{-x}{x+1}>0$在$[{-\frac{1}{2},-\frac{1}{3}}]$上恒成立,即$[{-\frac{1}{2},-\frac{1}{3}}]$为函数f(x)的单调递增区间,满足条件;
当a≠0时,由f′(x)=0,得x=0,或$x=-1-\frac{1}{2a}$.
若a>0,$-1-\frac{1}{2a}<-1$,由f′(x)>0,得-1<x<0,即f(x)在(-1,0)上单调递增,显然,$[{-\frac{1}{2},-\frac{1}{3}}]$为函数f(x)的单调递增区间;
若a<0,要使函数f(x)在$[{-\frac{1}{2},-\frac{1}{3}}]$上有单调递增区间,则f′(x)>0的解集与$({-\frac{1}{2},-\frac{1}{3}})$有公共区间,即$-1-\frac{1}{2a}>-\frac{1}{2}$,-1<a<0.
综上所述,若函数f(x)在区间$[{-\frac{1}{2},-\frac{1}{3}}]$上有单调递增区间,则实数a的取值范围为(-1,+∞);
证明:(Ⅱ)a=1时,在(0,+∞)上,f′(x)<0恒成立,即函数f(x)在区间(0,+∞)上单调递减,
∴x∈(0,+∞)时,f(x)<f(0)=0恒成立,
即 ln(1+x)-x-x2<0,
即ln(1+x)<x+x2在区间(0,+∞)上恒成立,
取x=n,n∈N*,则0<ln(1+n)<n+n2,
即$\frac{1}{ln(1+n)}>\frac{1}{{n+{n^2}}}$,
即$\frac{1}{ln(1+n)}>\frac{1}{n}-\frac{1}{n+1}$,
∴$\frac{1}{ln2}>\frac{1}{1}-\frac{1}{2}$,$\frac{1}{ln3}>\frac{1}{2}-\frac{1}{3}$,$\frac{1}{ln4}>\frac{1}{3}-\frac{1}{4}$,…,$\frac{1}{lnn}>\frac{1}{n-1}-\frac{1}{n}$,$\frac{1}{ln(1+n)}>\frac{1}{n}-\frac{1}{n+1}$.
∴$\frac{1}{ln2}+\frac{1}{ln3}+\frac{1}{ln4}…+\frac{1}{ln(n+1)}>1-\frac{1}{n+1}$,
即$\frac{1}{ln2}+\frac{1}{ln3}+\frac{1}{ln4}…+\frac{1}{ln(n+1)}>\frac{n}{n+1}$.
点评 本题考查利用导数研究函数的单调性,训练了利用导数证明函数不等式,体现了数学转化思想方法和分类讨论的数学思想方法,是压轴题.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案| A. | $\frac{1}{8}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{4}$ |
| A. | 2 | B. | $\sqrt{4+\frac{π^2}{9}}$ | C. | $\sqrt{1+\frac{π^2}{9}}$ | D. | $\sqrt{3}$ |
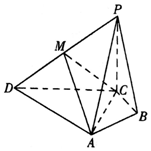 在四棱锥P-ABCD中,PC⊥底面ABCD,M是PD的中点,AC⊥AD,BA⊥BC,PC=AC=2BC,∠ACD=∠ACB.
在四棱锥P-ABCD中,PC⊥底面ABCD,M是PD的中点,AC⊥AD,BA⊥BC,PC=AC=2BC,∠ACD=∠ACB.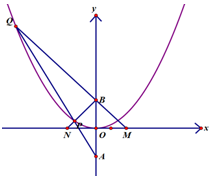 已知抛物线的方程为x2=2py(p>0),过点A(0,-a)(a>0)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,a),连接BP,BQ.且QB,QP与x轴分别交于M,N两点,如果QB的斜率与PB的斜率之积为-3,则∠PBQ=$\frac{2π}{3}$.
已知抛物线的方程为x2=2py(p>0),过点A(0,-a)(a>0)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,a),连接BP,BQ.且QB,QP与x轴分别交于M,N两点,如果QB的斜率与PB的斜率之积为-3,则∠PBQ=$\frac{2π}{3}$.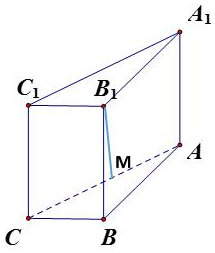 如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,BB1=5,AB=4,BC=2.
如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,BB1=5,AB=4,BC=2.