Question

已知平面区域如图，A（5，3），B（1，1），C（1，5），z=mx+y（m＞0）在平面区域内取得最大值时的最优解有无数多个，则m=______．

Answer 1

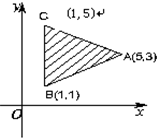
由z=mx+y（m＞0），得y=-mx+z，
∵m＞0，∴直线的斜率为-m＜0，
要使z=mx+y（m＞0）在平面区域内取得最大值时的最优解有无数多个，
即直线y=-mx+z和三角形的一个边平行，
即当-m=k_AC时，满足条件，
即-m=

5-3

1-5

=-

2

4

=-

1

2

，
解得m=

1

2

．
故答案为：

1

2

．