题目内容
已知数列{an}为等差数列,Sn为其前n项和,若S7=7,S15=75,
(1)求数列{an}的首项和公差;
(2)求数列{
}的前n项和Tn.
(1)求数列{an}的首项和公差;
(2)求数列{
| Sn |
| n |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件,利用等差数列前n项和公式列出方程组能求出数列{an}的首项和公差.
(2)由数列{an}的首项和公差,利用等差数列的前n项和公式,能推导出
=
,由此利用分组求和法能求出Tn.
(2)由数列{an}的首项和公差,利用等差数列的前n项和公式,能推导出
| Sn |
| n |
| n-5 |
| 2 |
解答:
解:(1)∵数列{an}为等差数列,Sn为其前n项和,S7=7,S15=75,
设数列的公差为d,
∴
,
解得a1=-2,d=1.
(2)∵a1=-2,d=1.
∴Sn=-2n+
×1=
,
∴
=
,
∴Tn=
(1+2+3+…+n)-
×n
=
×
-
=
n2-
n.
设数列的公差为d,
∴
|
解得a1=-2,d=1.
(2)∵a1=-2,d=1.
∴Sn=-2n+
| n(n-1) |
| 2 |
| n2-5n |
| 2 |
∴
| Sn |
| n |
| n-5 |
| 2 |
∴Tn=
| 1 |
| 2 |
| 5 |
| 2 |
=
| 1 |
| 2 |
| n(n+1) |
| 2 |
| 5n |
| 2 |
=
| 1 |
| 4 |
| 9 |
| 4 |
点评:本题考查等差数列的首项和公差的求法,考查数列前n项和的求法,是中档题,解题时要注意分组求和法的合理运用.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=a,E,F分别为AD,CD的中点.
在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=a,E,F分别为AD,CD的中点. 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=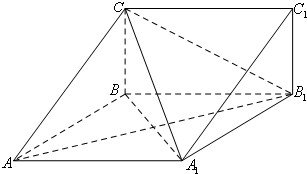 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=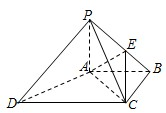 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=3,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=3,点E在棱PB上,且PE=2EB. 如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2
如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2