题目内容
14.已知方程x2-5x-8=0的两个根为x1,x2,求作一个新的一元二次方程,使它的两根分别为$\frac{{x}_{1}}{{x}_{2}}$和$\frac{{x}_{2}}{{x}_{1}}$.分析 根据一元二次方程根与系数之间的关系,求出$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$和$\frac{{x}_{1}}{{x}_{2}}$•$\frac{{x}_{2}}{{x}_{1}}$即可得到结论.
解答 解:∵方程x2-5x-8=0的两个根为x1,x2,
∴x1+x2=5,x1x2=-8,
则$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{x}_{1}{x}_{2}}$=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{25-2×(-8)}{-8}$=$\frac{25+16}{-8}$=-$\frac{41}{8}$,
$\frac{{x}_{1}}{{x}_{2}}$•$\frac{{x}_{2}}{{x}_{1}}$=1.
则以$\frac{{x}_{1}}{{x}_{2}}$和$\frac{{x}_{2}}{{x}_{1}}$为根的一元二次方程为x2-($\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$)x+$\frac{{x}_{1}}{{x}_{2}}$•$\frac{{x}_{2}}{{x}_{1}}$=0.
即x2+$\frac{41}{8}$x+1=0.
点评 本题主要考查一元二次方程的求解,根据一元二次方程根与系数之间的关系是解决本题的关键.

练习册系列答案
相关题目
 如图,点P为⊙O外一点,过点P作⊙O的两条切线,切点分别为A、B.过点A作PB的平行线,交⊙O于点C,连接PC,交⊙O于点E;连接AE,并延长AE交PB于点E,求证:PE•AC=CE•KB.
如图,点P为⊙O外一点,过点P作⊙O的两条切线,切点分别为A、B.过点A作PB的平行线,交⊙O于点C,连接PC,交⊙O于点E;连接AE,并延长AE交PB于点E,求证:PE•AC=CE•KB.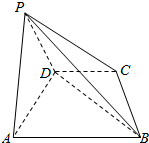 四棱锥P-ABCD中,△PAD为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.
四棱锥P-ABCD中,△PAD为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.