题目内容
5.已知函数f(x)=2ex-mx在区间[-1,0]上不单调,则实数m的取值范围为[$\frac{2}{e}$,2].分析 先求导数,f′(x)=2ex-m,根据f(x)在[-1,0]上不单调,从而有f′(x)=0在[-1,0]上有解,从而可得到m=2ex,这样根据x的范围即可求出实数m的范围.
解答 解:f′(x)=2ex-m;
f(x)在[-1,0]上不单调;
∴f(x)在[-1,0]上有极值;
即方程2ex-m=0在[-1,0]上有解;
∴m=2ex,x∈[-1,0];
∴2e-1≤m≤2e0;
∴$\frac{2}{e}≤m≤2$;
∴实数m的取值范围为:$[\frac{2}{e},2]$.
故答案为:[$\frac{2}{e}$,2].
点评 考查函数单调性的定义,函数导数符号和函数单调性的关系,以及函数极值的概念及判断方法,指数函数的单调性.

练习册系列答案
相关题目
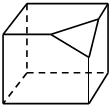
16.图是截去了一个角的正方体,则它的俯视图为( )

| A. | 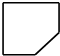 | B. | 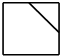 | C. | 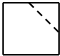 | D. | 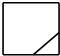 |
14.下面程序的功能是( )
INPUT“n=“;n
A=1
i=1
WHILE i<=n
A=A*i
i=i+1
WEND
PRINT A
END.
INPUT“n=“;n
A=1
i=1
WHILE i<=n
A=A*i
i=i+1
WEND
PRINT A
END.
| A. | 计算1+2+…+n | B. | 计算1+(1+2)+(1+2+3)+…(1+2+3+…+n) | ||
| C. | 计算n! | D. | 以上都不对 |
17.参数方程$\left\{\begin{array}{l}{x=2+si{n}^{2}θ}\\{y=-1+2co{s}^{2}θ}\end{array}\right.$(θ为参数)化为普通方程是( )
| A. | 2x-y+5=0 | B. | 2x+y-5=0 | C. | 2x-y+5=0(2≤x≤3) | D. | 2x+y-5=0(2≤x≤3) |
14.已知方程x2-5x-8=0的两个根为x1,x2,求作一个新的一元二次方程,使它的两根分别为$\frac{{x}_{1}}{{x}_{2}}$和$\frac{{x}_{2}}{{x}_{1}}$.
15.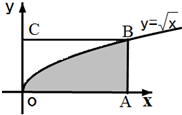 如图,长方形的四个顶点为O(0,0),A(4,0),B(4,2),C(0,2),曲线$y=\sqrt{x}$经过点B,现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是( )
如图,长方形的四个顶点为O(0,0),A(4,0),B(4,2),C(0,2),曲线$y=\sqrt{x}$经过点B,现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是( )
 如图,长方形的四个顶点为O(0,0),A(4,0),B(4,2),C(0,2),曲线$y=\sqrt{x}$经过点B,现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是( )
如图,长方形的四个顶点为O(0,0),A(4,0),B(4,2),C(0,2),曲线$y=\sqrt{x}$经过点B,现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{7}$ | D. | $\frac{7}{12}$ |