题目内容
9.已知一元二次方程x2+ax+b=0的一个根在[-2,-1]内,另一个根在[1,2]内,使用图表示出以a,b为坐标轴的点(a,b)的存在范围,并求a+b的取值范围.分析 设f(x)=x2+ax+b,根据根与系数之间建立不等式关系,作出不等式组对应的平面区域,利用线性规划的知识进行求解即可.
解答 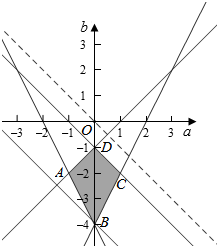 解:设f(x)=x2+ax+b,
解:设f(x)=x2+ax+b,
∵元二次方程x2+ax+b=0的一个根在[-2,-1]内,另一个根在[1,2]内,
∴$\left\{\begin{array}{l}{f(-1)≤0}\\{f(-2)≥0}\\{f(1)≤0}\\{f(2)≥0}\end{array}\right.$,即$\left\{\begin{array}{l}{1-a+b≤0}\\{4-2a+b≥0}\\{1+a+b≤0}\\{4+2a+b≥0}\end{array}\right.$,
作出不等式组对应的平面区域如图:
则以a,b为坐标轴的点(a,b)的存在区域为四边形ABCD及其内部,
设z=a+b,即b=-a+z,
平移直线b=-a+z,
由图象知当直线b=-a+z经过点B(0,-4)时,直线b=-a+z的截距最小,此时z最小,z=0-4=-4,
当直线b=-a+z与直线CD:a+b+1=0重合是,直线b=-a+z的截距最大,此时z=-1,
即-4≤z≤-1,
即a+b的取值范围是[-4,-1].
点评 本题主要考查线性规划的应用,利用一元二次方程根与系数之间的关系,将方程转化为函数,利用一元二次函数的性质是解决本题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
17.参数方程$\left\{\begin{array}{l}{x=2+si{n}^{2}θ}\\{y=-1+2co{s}^{2}θ}\end{array}\right.$(θ为参数)化为普通方程是( )
| A. | 2x-y+5=0 | B. | 2x+y-5=0 | C. | 2x-y+5=0(2≤x≤3) | D. | 2x+y-5=0(2≤x≤3) |
14.已知方程x2-5x-8=0的两个根为x1,x2,求作一个新的一元二次方程,使它的两根分别为$\frac{{x}_{1}}{{x}_{2}}$和$\frac{{x}_{2}}{{x}_{1}}$.
18.方程-sinx=($\frac{1}{2}$)x在区间(0,100π)内解的个数是( )
| A. | 98 | B. | 100 | C. | 102 | D. | 200 |
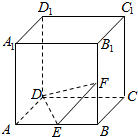 如图,正方体ABCD-A1B1C1D1中,E,F分别为AB与BB1的中点.
如图,正方体ABCD-A1B1C1D1中,E,F分别为AB与BB1的中点.