题目内容
3．已知奇函数f（x）是定义域为（-3，3）上的减函数，若f（1-2x）+f（3-x）＜0，求x的取值范围．分析 根据函数奇偶性和单调性的关系进行求解即可．
解答 解：∵奇函数f（x）是（-3，3）上的减函数，
∴由f（1-2x）+f（3-x）＜0得f（3-x）＜-f（1-2x）=f（2x-1），
即$\left\{\begin{array}{l}{-3＜1-2x＜3}\\{-3＜3-x＜3}\\{3-x＞2x-1}\end{array}\right.$，即$\left\{\begin{array}{l}{-2＜2x＜4}\\{0＜x＜3}\\{3x＜4}\end{array}\right.$，即$\left\{\begin{array}{l}{-1＜x＜2}\\{0＜x＜3}\\{x＜\frac{4}{3}}\end{array}\right.$，
解得0＜x＜$\frac{4}{3}$，
即实数x的取值范围是（0，$\frac{4}{3}$）．
点评 本题主要考查不等式的求解，根据函数奇偶性和单调性之间的关系是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
14．下面程序的功能是（ ）
INPUT“n=“；n
A=1
i=1
WHILE i＜=n
A=A*i
i=i+1
WEND
PRINT A
END．
INPUT“n=“；n
A=1
i=1
WHILE i＜=n
A=A*i
i=i+1
WEND
PRINT A
END．
| A． | 计算1+2+…+n | B． | 计算1+（1+2）+（1+2+3）+…（1+2+3+…+n） | ||
| C． | 计算n! | D． | 以上都不对 |
14．已知方程x2-5x-8=0的两个根为x1，x2，求作一个新的一元二次方程，使它的两根分别为$\frac{{x}_{1}}{{x}_{2}}$和$\frac{{x}_{2}}{{x}_{1}}$．
18．方程-sinx=（$\frac{1}{2}$）x在区间（0，100π）内解的个数是（ ）
| A． | 98 | B． | 100 | C． | 102 | D． | 200 |
15．
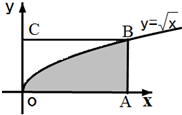如图，长方形的四个顶点为O（0，0），A（4，0），B（4，2），C（0，2），曲线$y=\sqrt{x}$经过点B，现将一质点随机投入长方形OABC中，则质点落在图中阴影区域的概率是（ ）
如图，长方形的四个顶点为O（0，0），A（4，0），B（4，2），C（0，2），曲线$y=\sqrt{x}$经过点B，现将一质点随机投入长方形OABC中，则质点落在图中阴影区域的概率是（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{7}$ | D． | $\frac{7}{12}$ |