题目内容
2.已知以极点为原点,极轴为x轴正方向建立即坐标系,曲线C1的极坐标方程是ρ=4cosθ,直线l的参数方程是$\left\{\begin{array}{l}{x=2+tcosθ}\\{y=1+tsinθ}\end{array}\right.$(t为参数).(1)求曲线C1的直角坐标方程;
(2)设直线l与曲线C1交于A,B两点,点M的直角坐标为(2,1),若$\overrightarrow{AB}$=3$\overrightarrow{MB}$,求直线l的普通方程.
分析 (1)利用直角坐标与极坐标间的关系:ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.
(2)设A(2+tAcosθ,1+tAsinθ),B(2+tBcosθ,1+tBsinθ).把直线的参数方程代入曲线C1的方程,根据t的几何意义即可求出.
解答 解:(1)由ρ=4cosθ,得ρ2=4ρcosθ,
∵ρ2=x2+y2,x=ρcosθ
∴曲线C1的直角坐标方程是x2+y2=4x,
即(x-2)2+y2=4(4分)
(2)设A(2+tAcosθ,1+tAsinθ),B(2+tBcosθ,1+tBsinθ)
由已知|$\overrightarrow{MA}$|=2|$\overrightarrow{MB}$|,注意到M(2,1)是直线参数方程恒过的定点,
∴tA=-2tB①
联立直线的参数方程与曲线C1的直角坐标方程得:t2cos2θ+(1+tsinθ)2=4,
整理得:t2+2tsinθ-3=0,(6分)
∴tA+tB=-2sinθ,tA•tB=-3,与①联立得:sinθ=$\frac{\sqrt{6}}{4}$,cosθ=±$\frac{\sqrt{10}}{4}$
∴直线的参数方程为$\left\{\begin{array}{l}{x=2+\frac{\sqrt{10}}{4}t}\\{y=1+\frac{\sqrt{6}}{4}t}\end{array}\right.$,(为参数)或$\left\{\begin{array}{l}{x=2-\frac{\sqrt{10}}{4}t}\\{y=1+\frac{\sqrt{6}}{4}t}\end{array}\right.$,(为参数).(8分)
消去参数得的普通方程为y=$\frac{\sqrt{15}}{5}$x-$\frac{2\sqrt{15}}{5}$+1或y=-$\frac{\sqrt{15}}{5}$x+$\frac{2\sqrt{15}}{5}$+1(10分)
点评 本题考查了极坐标、直角坐标方程、及参数方程的互化,考查了方程思想,属于基础题.

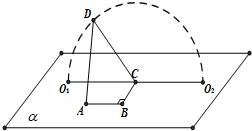 如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )
如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )| A. | 一直变小 | B. | 一直变大 | ||
| C. | 先变小,后变大 | D. | 先变小,再变大,后变小 |
INPUT“n=“;n
A=1
i=1
WHILE i<=n
A=A*i
i=i+1
WEND
PRINT A
END.
| A. | 计算1+2+…+n | B. | 计算1+(1+2)+(1+2+3)+…(1+2+3+…+n) | ||
| C. | 计算n! | D. | 以上都不对 |
| A. | 2x-y+5=0 | B. | 2x+y-5=0 | C. | 2x-y+5=0(2≤x≤3) | D. | 2x+y-5=0(2≤x≤3) |