题目内容
空间直角坐标系中与点P（2，3，5）关于yOz平面对称的点为P′，则|PP′|= ．
考点：空间两点间的距离公式,空间中的点的坐标
专题：空间位置关系与距离
分析：根据关于yOz平面对称，x值变为相反数，求出P′的坐标，然后求解距离即可．
解答：
解：根据关于坐标平面yOz的对称点的坐标的特点，
可得点P（2，3，5）关于坐标平面yOz的对称点的坐标为P′：（-2，3，5）．
|PP′|=2+2=4．
故答案为：4．
可得点P（2，3，5）关于坐标平面yOz的对称点的坐标为P′：（-2，3，5）．
|PP′|=2+2=4．
故答案为：4．
点评：本题考查空间向量的坐标的概念，考查空间点的对称点的坐标的求法，距离公式的应用，属于基础题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
已知函数f（x）对于任意的x∈R都有f（x）＜f（x+1），则f（x）在R上（ ）
| A、是单调增函数 |
| B、没有单调减区间 |
| C、可能存在单调增区间，也可能不存在单调增区间 |
| D、没有单调增区间 |
如图为函数f（x）=t+logax的图象（a，t均为实常数），则下列结论正确的是 （ ）
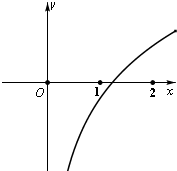
| A、0＜a＜1，t＜0 |
| B、0＜a＜1，t＞0 |
| C、a＞1，t＜0 |
| D、a＞1，t＞0 |