题目内容
8.若m是方程4${\;}^{x+\frac{1}{2}}$-9•2x+4=0的根,则圆锥曲线x2+$\frac{{y}^{2}}{m}$=1的离心率是$\frac{\sqrt{2}}{2}$或$\sqrt{2}$.分析 求出方程的两个根,得到曲线的方程,然后求解离心率即可.
解答 解:∵m是方程4${\;}^{x+\frac{1}{2}}$-9•2x+4=0的根,∴(2x-4)(2•2x-1)=0,
解之得x=2或x=-1,即m=2或m=-1..
当m=2时,曲线x2+$\frac{{y}^{2}}{m}$=1,即x2+$\frac{{y}^{2}}{2}$=1,表示焦点在y轴上的椭圆,
∵a12=2且b12=1,∴a1=$\sqrt{2}$,c1=$\sqrt{{{a}_{1}}^{2}+{{b}_{1}}^{2}}$=1,椭圆的离心率e1=$\frac{{c}_{1}}{{a}_{1}}$=$\frac{\sqrt{2}}{2}$;
当m=-1时,曲线x2+$\frac{{y}^{2}}{m}$=1,即x2-y2=1,表示焦点在x轴上的双曲线,
同理可得a2=1,b2=1,c2=$\sqrt{{{a}_{2}}^{2}+{{b}_{2}}^{2}}$=$\sqrt{2}$,双曲线的离心率e2=$\frac{{c}_{2}}{{a}_{2}}$=$\sqrt{2}$.
综上所述,圆锥曲线x2+$\frac{{y}^{2}}{m}$=1的离心率是:$\frac{\sqrt{2}}{2}$或$\sqrt{2}$.
故答案为:$\frac{\sqrt{2}}{2}$或$\sqrt{2}$.
点评 本题考查圆锥曲线的方程的求法,离心率的求法,考查计算能力.

练习册系列答案
相关题目
19.已知数列{an}的通项公式为${a_n}={({\frac{3}{4}})^{n-1}}[{{{({\frac{3}{4}})}^{n-1}}-1}]$,则关于an的最大项、最小项叙述正确的是( )
| A. | 最大项为a1、最小项为a3 | B. | 最大项为a1、最小项不存在 | ||
| C. | 最大项不存在、最小项为a3 | D. | 最大项为a1、最小项为a4 |
13.已知双曲线x2-y2=1,点F1,F2为其两个焦点,点P为双曲线上一点,若∠F1PF2=60°,则三角形F1PF2的面积为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
20.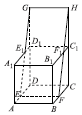 如图所示,在棱长为a的正方体ABCD-A1B2C3D4中,点E,F分别在棱AD,BC上,且AE=BF=$\frac{1}{3}$a.过EF的平面绕EF旋转,与DD1、CC1的延长线分别交于G,H点,与A1D1、B1C1分别交于E1,F1点.当异面直线FF1与DD1所成的角的正切值为$\frac{1}{3}$时,|GF1|=( )
如图所示,在棱长为a的正方体ABCD-A1B2C3D4中,点E,F分别在棱AD,BC上,且AE=BF=$\frac{1}{3}$a.过EF的平面绕EF旋转,与DD1、CC1的延长线分别交于G,H点,与A1D1、B1C1分别交于E1,F1点.当异面直线FF1与DD1所成的角的正切值为$\frac{1}{3}$时,|GF1|=( )
 如图所示,在棱长为a的正方体ABCD-A1B2C3D4中,点E,F分别在棱AD,BC上,且AE=BF=$\frac{1}{3}$a.过EF的平面绕EF旋转,与DD1、CC1的延长线分别交于G,H点,与A1D1、B1C1分别交于E1,F1点.当异面直线FF1与DD1所成的角的正切值为$\frac{1}{3}$时,|GF1|=( )
如图所示,在棱长为a的正方体ABCD-A1B2C3D4中,点E,F分别在棱AD,BC上,且AE=BF=$\frac{1}{3}$a.过EF的平面绕EF旋转,与DD1、CC1的延长线分别交于G,H点,与A1D1、B1C1分别交于E1,F1点.当异面直线FF1与DD1所成的角的正切值为$\frac{1}{3}$时,|GF1|=( )| A. | $\frac{\sqrt{19}a}{3}$ | B. | $\frac{\sqrt{19}a}{9}$ | C. | $\frac{\sqrt{2}a}{3}$ | D. | $\frac{\sqrt{2}a}{9}$ |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点与抛物线${y^2}=8\sqrt{2}x$的焦点相同,F1,F2为椭圆的左、右焦点.M为椭圆上任意一点,△MF1F2面积的最大值为4$\sqrt{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点与抛物线${y^2}=8\sqrt{2}x$的焦点相同,F1,F2为椭圆的左、右焦点.M为椭圆上任意一点,△MF1F2面积的最大值为4$\sqrt{2}$.