题目内容
【题目】设![]() 为等差数列
为等差数列![]() 的前
的前![]() 项和,且
项和,且![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若满足不等式![]() 的正整数
的正整数![]() 恰有
恰有![]() 个,求正实数
个,求正实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设等差数列![]() 的公差为
的公差为![]() ,根据题意得出关于
,根据题意得出关于![]() 和
和![]() 的方程组,解出这两个量的值,然后利用等差数列的通项公式可得出数列
的方程组,解出这两个量的值,然后利用等差数列的通项公式可得出数列![]() 的通项公式;
的通项公式;
(2)求出![]() ,可得出
,可得出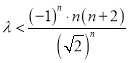 ,可知当
,可知当![]() 为奇数时不等式不成立,只考虑
为奇数时不等式不成立,只考虑![]() 为偶数的情况,利用数列单调性的定义判断数列
为偶数的情况,利用数列单调性的定义判断数列![]() 中偶数项构成的数列的单调性,由此能求出正实数
中偶数项构成的数列的单调性,由此能求出正实数![]() 的取值范围.
的取值范围.
(1)设等差数列![]() 的公差为
的公差为![]() ,
,
则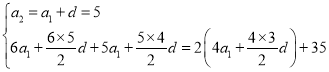 ,整理得
,整理得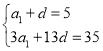 ,
,
解得![]() ,
,![]() ,因此,
,因此,![]() ;
;
(2)![]() ,
,
满足不等式![]() 的正整数
的正整数![]() 恰有
恰有![]() 个,得
个,得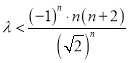 ,
,
由于![]() ,若
,若![]() 为奇数,则不等式
为奇数,则不等式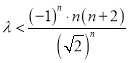 不可能成立.
不可能成立.
只考虑![]() 为偶数的情况,令
为偶数的情况,令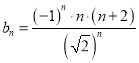 ,
,
则![]() ,
,![]() .
.
![]() .
.
当![]() 时,
时,![]() ,则
,则![]() ;
;
当![]() 时,
时,![]() ,则
,则![]() ;
;
当![]() 时,
时,![]() ,则
,则![]() .
.
所以,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】自2016年1月1日全面实施二孩政策以来,为了了解生二孩意愿与年龄段是否有关,某市选取“75后”和“80后”两个年龄段的已婚妇女作为调查对象,进行了问卷调查,共调查了40名“80后”,40名“75后”,其中调查的“80后”有10名不愿意生二孩,其余的全部愿意生二孩;调查的“75后”有5人不愿意生二孩,其余的全部愿意生二孩.
(1)根据以上数据完成下列![]() 列联表;
列联表;
年龄段 | 不愿意 | 愿意 | 合计 |
“80后” | |||
“75后” | |||
合计 |
(2)根据![]() 列联表,能否在犯错误的概率不超过0.05的前提下,认为“生二孩意愿与年龄段有关”?请说明理由.
列联表,能否在犯错误的概率不超过0.05的前提下,认为“生二孩意愿与年龄段有关”?请说明理由.
参考公式: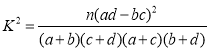 (其中
(其中![]() )
)
附表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |