题目内容
若实数x、y、m满足|x-m|>|y-m|,则称x比y远离m.
(1) 若x2-1比1远离0,求x的取值范围;
(2) 对任意两个不相等的正数a、b,证明:a3+b3比a2b+ab2远离2ab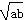 .
.
(1) 解:x∈(-∞,- )∪(
)∪( ,+∞).
,+∞).
(2) 证明:对任意两个不相等的正数a、b,有
a3+b3>2ab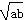 ,a2b+ab2>2ab
,a2b+ab2>2ab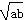 .
.
因为|a3+b3-2ab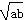 |-|a2b+ab2-2ab
|-|a2b+ab2-2ab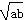 |=(a+b)(a-b)2>0,所以|a3+b3-2ab
|=(a+b)(a-b)2>0,所以|a3+b3-2ab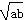 |>|a2b+ab2-2ab
|>|a2b+ab2-2ab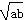 |,即a3+b3比a2b+ab2远离2ab
|,即a3+b3比a2b+ab2远离2ab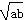 .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
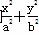 =1(a>b>0)的左、右焦点,点M在x轴上,且
=1(a>b>0)的左、右焦点,点M在x轴上,且 ,过点F2的直线与椭圆交于A、B两点,且AM⊥x轴,
,过点F2的直线与椭圆交于A、B两点,且AM⊥x轴,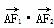 =0.
=0.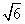 ,求椭圆的方程.
,求椭圆的方程.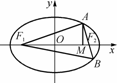
 ×底×高,可得扇形的面积公式为________.
×底×高,可得扇形的面积公式为________. ”时,假设的内容应为______________.
”时,假设的内容应为______________. ,
, 不能为同一等差数列中的三项.
不能为同一等差数列中的三项. +
+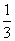 +…+
+…+ (n∈N),则n=1时,f(n)=________.
(n∈N),则n=1时,f(n)=________. ,试比较f(n)与
,试比较f(n)与 的大小.
的大小. 的值为6,那么运行相应程序,输出的
的值为6,那么运行相应程序,输出的 的值为
的值为
 x,x
x,x 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的