题目内容
如图,F1、F2是椭圆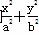 =1(a>b>0)的左、右焦点,点M在x轴上,且
=1(a>b>0)的左、右焦点,点M在x轴上,且 ,过点F2的直线与椭圆交于A、B两点,且AM⊥x轴,
,过点F2的直线与椭圆交于A、B两点,且AM⊥x轴,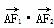 =0.
=0.
(1) 求椭圆的离心率;
(2) 若△ABF1的周长为4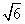 ,求椭圆的方程.
,求椭圆的方程.
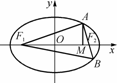
解:(1) 设F1(-c,0),F2(c,0),A(x0,y0),椭圆的离心率为e,则M .
.
∵ =e,∴ |AF1|=a+ex0.同理,|AF2|=a-ex0.
=e,∴ |AF1|=a+ex0.同理,|AF2|=a-ex0.
∵ =0,∴ AF1⊥AF2,
=0,∴ AF1⊥AF2,
∴ |AF1|2+|AF2|2=|F1F2|2,
∴ (a+ex0)2+(a-ex0)2=4c2, 即a2+e2x =2c2.
=2c2.
∵ x0=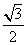 c,∴ a2+e2·
c,∴ a2+e2·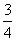 c2=2c2,
c2=2c2,
∴ 1+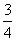 e4=2e2,即3e4-8e2+4=0,
e4=2e2,即3e4-8e2+4=0,
∴ e2= 或2(舍),∴ 椭圆的离心率e=
或2(舍),∴ 椭圆的离心率e= .
.
(2) ∵ △ABF2的周长为4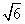 ,∴ 4a=4
,∴ 4a=4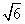 ,
,
∴ a=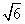 .又
.又 =
= ,∴ c=2, ∴ b2=2.
,∴ c=2, ∴ b2=2.
∴ 椭圆方程为 =1.
=1.

练习册系列答案
相关题目
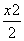 +y2=1的两焦点为F1,F2,点P(x0,y0)满足
+y2=1的两焦点为F1,F2,点P(x0,y0)满足 +y
+y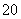 ≤1,则PF1+PF2的取值范围为________.
≤1,则PF1+PF2的取值范围为________.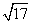 ,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.
,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.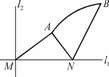
 =1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:
=1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G: (c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.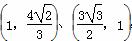 ,求椭圆C的方程;
,求椭圆C的方程;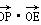 的值(O是坐标原点);
的值(O是坐标原点);
 在椭圆上.
在椭圆上.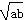 .
.